Scientific notation is the expression of a number 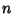 in the form
in the form 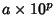 , where
, where
is the Floor of the base-10 Logarithm of 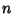 (the ``order of magnitude''), and
(the ``order of magnitude''), and
is a Real Number satisfying 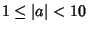 . For example, in scientific notation, the number
. For example, in scientific notation, the number 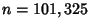 has order
of magnitude
has order
of magnitude
so 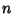 would be written
would be written
 . The special case of 0 does not have a unique representation in scientific
notation, i.e.,
. The special case of 0 does not have a unique representation in scientific
notation, i.e.,
 .
.
See also Characteristic (Real Number), Figures, Mantissa, Significant Digits
© 1996-9 Eric W. Weisstein
1999-05-26
![]() in the form
in the form ![]() , where
, where