|
|
|
Given a function
![]() , write
, write
![]() and define the Sturm functions by
and define the Sturm functions by
| (1) |
| (2) | |||
Sturm functions provide a convenient way for finding the number of real roots of an algebraic equation with real coefficients
over a given interval. Specifically, the difference in the number of sign changes between the Sturm functions evaluated at two
points ![]() and
and ![]() gives the number of real roots in the interval
gives the number of real roots in the interval ![]() . This powerful result is known as the Sturm
Theorem.
. This powerful result is known as the Sturm
Theorem.
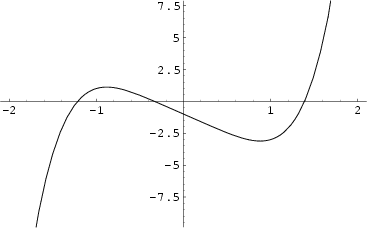
As a specific application of Sturm functions toward finding Polynomial Roots, consider the function
![]() ,
plotted above, which has roots
,
plotted above, which has roots ![]() ,
, ![]() ,
,
![]() , and 1.38879 (three of which are real). The
Derivative is given by
, and 1.38879 (three of which are real). The
Derivative is given by ![]() , and the Sturm Chain is then given by
, and the Sturm Chain is then given by
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
| 1 | 1 | 3 | |||
| 0 | 1 | 1 | 1 | ||
| 2 | 1 | 1 | 1 | 1 | 0 |
This shows that ![]() real roots lie in
real roots lie in ![]() , and
, and ![]() real root lies in
real root lies in ![]() . Reducing the spacing to
. Reducing the spacing to ![]() gives the following table.
gives the following table.
| 1 | 1 | 3 | |||
| 1 | 1 | 3 | |||
| 1 | 1 | 1 | 2 | ||
| 1 | 1 | 2 | |||
| 0.0 | 1 | 1 | 1 | ||
| 0.5 | 1 | 1 | 1 | ||
| 1.0 | 1 | 1 | 1 | 1 | |
| 1.5 | 1 | 1 | 1 | 1 | 0 |
| 2.0 | 1 | 1 | 1 | 1 | 0 |
This table isolates the three real roots and shows that they lie in the intervals ![]() ,
, ![]() , and
, and ![]() . If
desired, the intervals in which the roots fall could be further reduced.
. If
desired, the intervals in which the roots fall could be further reduced.
The Sturm functions satisfy the following conditions:
See also Descartes' Sign Rule, Sturm Chain, Sturm Theorem
References
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 334, 1990.
Dörrie, H. ``Sturm's Problem of the Number of Roots.'' §24 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 112-116, 1965.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, p. 469, 1992.
Rusin, D. ``Known Math.'' http://www.math.niu.edu./~rusin/known-math/polynomials/sturm.
Sturm, C. ``Mémoire sur la résolution des équations numériques.'' Bull. des sciences de Férussac 11, 1929.
|
|
|
© 1996-9 Eric W. Weisstein