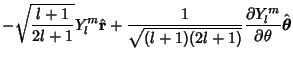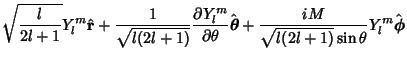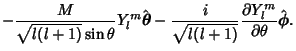The Spherical Harmonics can be generalized to vector spherical harmonics by looking for
a Scalar Function 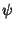 and a constant Vector
and a constant Vector 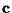 such that
such that
so
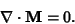 |
(2) |
Now use the vector identities
so
![\begin{displaymath}
\nabla^2{\bf M}+k^2{\bf M}=\nabla\times[{\bf c}(\nabla^2\psi+k^2\psi)],
\end{displaymath}](v_517.gif) |
(5) |
and 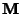 satisfies the vector Helmholtz Differential Equation if
satisfies the vector Helmholtz Differential Equation if 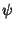 satisfies the scalar Helmholtz
Differential Equation
satisfies the scalar Helmholtz
Differential Equation
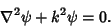 |
(6) |
Construct another vector function
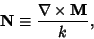 |
(7) |
which also satisfies the vector Helmholtz Differential Equation since
which gives
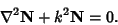 |
(9) |
We have the additional identity
In this formalism, 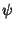 is called the generating function and
is called the generating function and 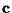 is called the Pilot Vector. The choice
of generating function is determined by the symmetry of the scalar equation, i.e., it is chosen to solve the desired
scalar differential equation. If
is called the Pilot Vector. The choice
of generating function is determined by the symmetry of the scalar equation, i.e., it is chosen to solve the desired
scalar differential equation. If 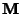 is taken as
is taken as
 |
(11) |
where 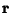 is the radius vector, then
is the radius vector, then 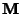 is a solution to the vector wave equation in spherical coordinates. If
we want vector solutions which are tangential to the radius vector,
is a solution to the vector wave equation in spherical coordinates. If
we want vector solutions which are tangential to the radius vector,
 |
(12) |
so
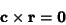 |
(13) |
and we may take
 |
(14) |
(Arfken 1985, pp. 707-711; Bohren and Huffman 1983, p. 88).
A number of conventions are in use. Hill (1954) defines
Morse and Feshbach (1953) define vector harmonics called 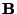 ,
, 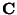 , and
, and 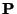 using rather complicated
expressions.
using rather complicated
expressions.
References
Arfken, G. ``Vector Spherical Harmonics.'' §12.11 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 707-711, 1985.
Blatt, J. M. and Weisskopf, V. ``Vector Spherical Harmonics.'' Appendix B, §1 in
Theoretical Nuclear Physics. New York: Wiley, pp. 796-799, 1952.
Bohren, C. F. and Huffman, D. R. Absorption and Scattering of Light by Small Particles.
New York: Wiley, 1983.
Hill, E. H. ``The Theory of Vector Spherical Harmonics.'' Amer. J. Phys. 22, 211-214, 1954.
Jackson, J. D. Classical Electrodynamics, 2nd ed. New York: Wiley, pp. 744-755, 1975.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part II. New York: McGraw-Hill, pp. 1898-1901, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and a constant Vector
and a constant Vector ![]() such that
such that
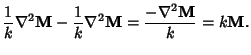
![]() is called the generating function and
is called the generating function and ![]() is called the Pilot Vector. The choice
of generating function is determined by the symmetry of the scalar equation, i.e., it is chosen to solve the desired
scalar differential equation. If
is called the Pilot Vector. The choice
of generating function is determined by the symmetry of the scalar equation, i.e., it is chosen to solve the desired
scalar differential equation. If ![]() is taken as
is taken as