If 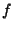 is a continuous real-valued function on
is a continuous real-valued function on ![$[a,b]$](w_463.gif) and if any
and if any 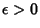 is given, then there exists a
Polynomial
is given, then there exists a
Polynomial 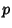 on
on ![$[a,b]$](w_463.gif) such that
such that
for all ![$x\in[a,b]$](w_465.gif) . In words, any continuous function on a closed and bounded interval can be
uniformly approximated on that interval by Polynomials to any degree of accuracy.
. In words, any continuous function on a closed and bounded interval can be
uniformly approximated on that interval by Polynomials to any degree of accuracy.
See also Müntz's Theorem
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is a continuous real-valued function on
is a continuous real-valued function on ![]() and if any
and if any ![]() is given, then there exists a
Polynomial
is given, then there exists a
Polynomial ![]() on
on ![]() such that
such that