|
|
|
Müntz's theorem is a generalization of the Weierstraß Approximation Theorem, which states that any continuous function on a closed and bounded interval can be uniformly approximated by Polynomials involving constants and any Infinite Sequence of Powers whose Reciprocals diverge.
In technical language, Müntz's theorem states that the Müntz Space ![]() is dense in
is dense in
![]() Iff
Iff
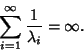
See also Weierstraß Approximation Theorem