Alexander's Horned Sphere

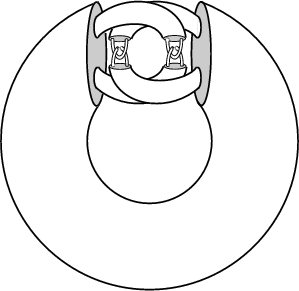
$\begin{figure}\begin{center}\BoxedEPSF{AlexandersHornedSphere.epsf}\end{center}\end{figure}$

The above solid, composed of a countable Union of Compact Sets, is called Alexander's horned sphere. It is Homeomorphic with the Ball $\Bbb{B}^3$ , and its boundary is therefore a Sphere. It is therefore an example of a wild embedding in $\Bbb{E}^3$ . The outer complement of the solid is not Simply Connected, and its fundamental Group is not finitely generated. Furthermore, the set of nonlocally flat (``bad'') points of Alexander's horned sphere is a Cantor Set.

The complement in $\Bbb{R}^3$ of the bad points for Alexander's horned sphere is Simply Connected, making it inequivalent to Antoine's Horned Sphere. Alexander's horned sphere has an uncountable infinity of Wild Points, which are the limits of the sequences of the horned sphere's branch points (roughly, the ``ends'' of the horns), since any Neighborhood of a limit contains a horned complex.

A humorous drawing by Simon Frazer (Guy 1983, Schroeder 1991, Albers 1994) depicts mathematician John H. Conway with Alexander's horned sphere growing from his head.

$\begin{figure}\begin{center}\BoxedEPSF{ConwaysHornedSphere.epsf scaled 750}\end{center}\end{figure}$

See also Antoine's Horned Sphere

References

Albers, D. J. Illustration accompanying ``The Game of `Life'.'' Math Horizons, p. 9, Spring 1994.

Guy, R. ``Conway's Prime Producing Machine.'' Math. Mag. 56, 26-33, 1983.

Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 80-81, 1976.

Schroeder, M. Fractals, Chaos, Power Law: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 58, 1991.