|
|
|
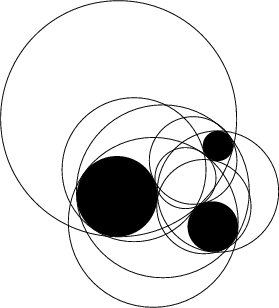
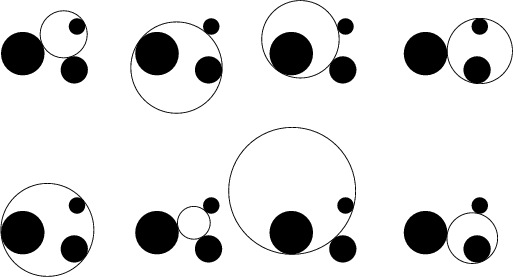
Given three objects, each of which may be a Point, Line, or Circle, draw a Circle that is
Tangent to each. There are a total of ten cases. The two easiest involve three points or three Lines,
and the hardest involves three Circles. Euclid ![]() solved the two easiest cases in his Elements, and the others (with the exception of the three Circle problem), appeared in the Tangencies of
Apollonius which was, however, lost. The general problem is, in principle, solvable by Straightedge and Compass
alone.
solved the two easiest cases in his Elements, and the others (with the exception of the three Circle problem), appeared in the Tangencies of
Apollonius which was, however, lost. The general problem is, in principle, solvable by Straightedge and Compass
alone.
The three-Circle problem was solved by Viète (Boyer 1968), and the solutions are called Apollonius Circles.
There are eight total solutions. The simplest solution is obtained by solving the three simultaneous quadratic equations
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
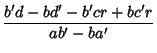 |
(11) | ||
 |
(12) |
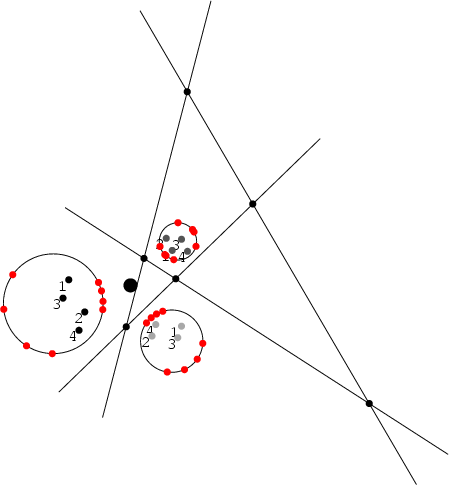
Perhaps the most elegant solution is due to Gergonne. It proceeds by locating the six Homothetic Centers (three internal and three external) of the three given Circles. These lie three by three on four lines (illustrated above). Determine the Poles of one of these with respect to each of the three Circles and connect the Poles with the Radical Center of the Circles. If the connectors meet, then the three pairs of intersections are the points of tangency of two of the eight circles (Johnson 1929, Dörrie 1965). To determine which two of the eight Apollonius circles are produced by the three pairs, simply take the two which intersect the original three Circles only in a single point of tangency. The procedure, when repeated, gives the other three pairs of Circles.
If the three Circles are mutually tangent, then the eight solutions collapse to two, known as the Soddy Circles.
See also Apollonius Pursuit Problem, Bend (Curvature), Casey's Theorem, Descartes Circle Theorem, Four Coins Problem, Hart's Theorem, Soddy Circles
References
Boyer, C. B. A History of Mathematics. New York: Wiley, p. 159, 1968.
Courant, R. and Robbins, H. ``Apollonius' Problem.'' §3.3 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 117 and 125-127, 1996.
Dörrie, H. ``The Tangency Problem of Apollonius.'' §32 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 154-160, 1965.
Gauss, C. F. Werke, Vol. 4. New York: George Olms, p. 399, 1981.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 118-121, 1929.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 48-51, 1990.
Pappas, T. The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 151, 1989.
Simon, M. Über die Entwicklung der Elementargeometrie im XIX Jahrhundert. Berlin, pp. 97-105, 1906.
![]() Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
|
|
|
© 1996-9 Eric W. Weisstein