A Map 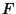 from
from 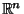 to
to 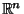 is Area-preserving if
is Area-preserving if
for every subregion 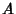 of
of 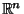 , where
, where 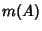 is the
is the 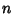 -D Measure of
-D Measure of 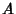 . A linear transformation is
Area-preserving if its corresponding Determinant is equal to 1.
. A linear transformation is
Area-preserving if its corresponding Determinant is equal to 1.
See also Conformal Map, Symplectic Map
© 1996-9 Eric W. Weisstein
1999-05-25
![]() from
from ![]() to
to ![]() is Area-preserving if
is Area-preserving if