|
|
|
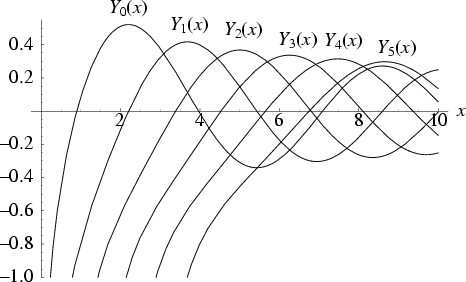
A Bessel function of the second kind ![]() is a solution to the Bessel Differential Equation which is singular at the
origin. Bessel functions of the second kind are also called Neumann Functions or Weber
Functions. The above plot shows
is a solution to the Bessel Differential Equation which is singular at the
origin. Bessel functions of the second kind are also called Neumann Functions or Weber
Functions. The above plot shows ![]() for
for ![]() , 2, ..., 5.
, 2, ..., 5.
Let
![]() be the first solution and
be the first solution and ![]() be the other one (since the Bessel Differential Equation is
second-order, there are two Linearly Independent solutions). Then
be the other one (since the Bessel Differential Equation is
second-order, there are two Linearly Independent solutions). Then
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
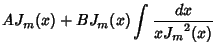 |
|||
| (7) |
|
|
|
|
|
|
|
|
(8) |
| (9) |
| (10) |
Asymptotic equations are
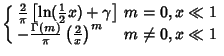 |
(11) | ||
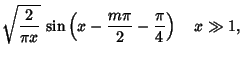 |
(12) |
See also Bessel Function of the First Kind, Bourget's Hypothesis, Hankel Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bessel Functions
Arfken, G. ``Neumann Functions, Bessel Functions of the Second Kind,
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 625-627, 1953.
Spanier, J. and Oldham, K. B. ``The Neumann Function
![]() and
and ![]() .''
§9.1 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972.
.''
§9.1 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972.
![]() .'' §11.3 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985.
.'' §11.3 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985.
![]() .''
Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987.
.''
Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987.
|
|
|
© 1996-9 Eric W. Weisstein