The differential equation obtained by applying the Biharmonic Operator and setting to zero.
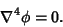 |
(1) |
In Cartesian Coordinates, the biharmonic equation is
In Polar Coordinates (Kaplan 1984, p. 148)
For a radial function 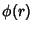 , the biharmonic equation becomes
, the biharmonic equation becomes
Writing the inhomogeneous equation as
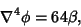 |
(5) |
we have
![\begin{displaymath}
64\beta r\,dr = d\left\{{r{d\over dr}\left[{{1\over r}{d\over dr}\left({r{d\phi\over dr}}\right)}\right]}\right\}
\end{displaymath}](b_1191.gif) |
(6) |
![\begin{displaymath}
32\beta r^2+C_1=r{d\over dr}\left[{{1\over r}{d\over dr}\left({r {d\phi\over dr}}\right)}\right]
\end{displaymath}](b_1192.gif) |
(7) |
![\begin{displaymath}
\left({32\beta r+{C_1\over r}}\right)\, dr=d\left[{{1\over r}{d\over dr}\left({r{d\phi\over dr}}\right)}\right]
\end{displaymath}](b_1193.gif) |
(8) |
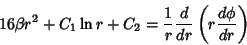 |
(9) |
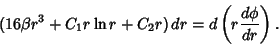 |
(10) |
Now use
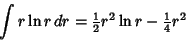 |
(11) |
to obtain
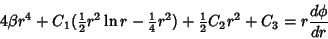 |
(12) |
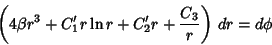 |
(13) |
The homogeneous biharmonic equation can be separated and solved in 2-D Bipolar Coordinates.
References
Kaplan, W. Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, 1991.
© 1996-9 Eric W. Weisstein
1999-05-26

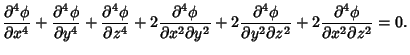
![$\displaystyle {1\over r}{d\over dr}\left\{{r{d\over dr}\left[{{1\over r}{d\over dr}\left({r{d\phi\over dr}}\right)}\right]}\right\}$](b_1188.gif)