|
|
|
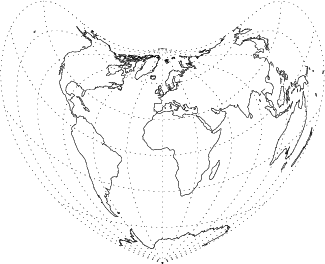
A Map Projection which resembles the shape of a heart. Let ![]() be the standard parallel and
be the standard parallel and ![]() the
central meridian. Then
the
central meridian. Then
| (1) | |||
| (2) |
| (3) | |||
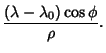 |
(4) |
| (5) | |||
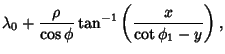 |
(6) |
| (7) |
References
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395. Washington,
DC: U. S. Government Printing Office, pp. 138-140, 1987.