|
|
|
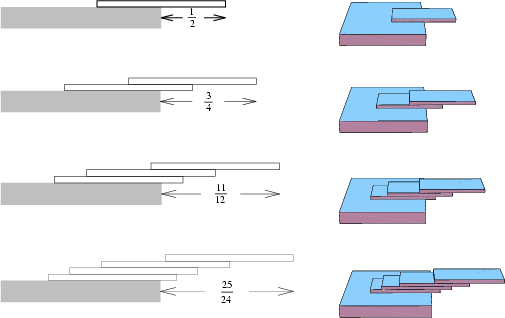
How far can a stack of ![]() books protrude over the edge of a table without the stack falling over? It turns out that the
maximum overhang possible
books protrude over the edge of a table without the stack falling over? It turns out that the
maximum overhang possible ![]() for
for ![]() books (in terms of book lengths) is half the
books (in terms of book lengths) is half the ![]() th partial sum of the Harmonic
Series, given explicitly by
th partial sum of the Harmonic
Series, given explicitly by
![\begin{displaymath}
d_n={1\over 2}\sum_{k=1}^n {1\over k}={\textstyle{1\over 2}}[\gamma+\Psi(1+n)]
\end{displaymath}](b_1779.gif)
In order to find the number of stacked books required to obtain ![]() book-lengths of overhang, solve the
book-lengths of overhang, solve the ![]() equation for
equation for
![]() , and take the Ceiling Function. For
, and take the Ceiling Function. For ![]() , 2, ... book-lengths of overhang, 4, 31, 227, 1674, 12367,
91380, 675214, 4989191, 36865412, 272400600, ... (Sloane's A014537) books are needed.
, 2, ... book-lengths of overhang, 4, 31, 227, 1674, 12367,
91380, 675214, 4989191, 36865412, 272400600, ... (Sloane's A014537) books are needed.
References
Dickau, R. M. ``The Book-Stacking Problem.''
http://www.prairienet.org/~pops/BookStacking.html.
Eisner, L. ``Leaning Tower of the Physical Review.'' Amer. J. Phys. 27, 121, 1959.
Gardner, M. Martin Gardner's Sixth Book of Mathematical Games from Scientific American.
New York: Scribner's, p. 167, 1971.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science.
Reading, MA: Addison-Wesley, pp. 272-274, 1990.
Johnson, P. B. ``Leaning Tower of Lire.'' Amer. J. Phys. 23, 240, 1955.
Sharp, R. T. ``Problem 52.'' Pi Mu Epsilon J. 1, 322, 1953.
Sharp, R. T. ``Problem 52.'' Pi Mu Epsilon J. 2, 411, 1954.
Sloane, N. J. A. Sequences
A014537,
A001008/M2885, and
A002805/M1589,
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein