|
|
|
Take ![]() itself to be a bracketing, then recursively define a bracketing as a sequence
itself to be a bracketing, then recursively define a bracketing as a sequence
![]() where
where ![]() and
each
and
each ![]() is a bracketing. A bracketing can be represented as a parenthesized string of
is a bracketing. A bracketing can be represented as a parenthesized string of ![]() s, with parentheses removed from
any single letter
s, with parentheses removed from
any single letter ![]() for clarity of notation (Stanley 1997). Bracketings built up of binary operations only are called
Binary Bracketings. For example, four letters have 11 possible bracketings:
for clarity of notation (Stanley 1997). Bracketings built up of binary operations only are called
Binary Bracketings. For example, four letters have 11 possible bracketings:
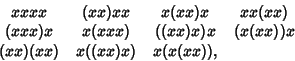
The number of bracketings on ![]() letters is given by the Generating Function
letters is given by the Generating Function
The first Plutarch Number 103,049 is equal to ![]() (Stanley 1997), suggesting that
Plutarch's problem of ten compound propositions is equivalent to the number of bracketings. In addition, Plutarch's second
number 310,954 is given by
(Stanley 1997), suggesting that
Plutarch's problem of ten compound propositions is equivalent to the number of bracketings. In addition, Plutarch's second
number 310,954 is given by
![]() (Habsieger et al. 1998).
(Habsieger et al. 1998).
See also Binary Bracketing, Plutarch Numbers
References
Habsieger, L.; Kazarian, M.; and Lando, S. ``On the Second Number of Plutarch.'' Amer. Math. Monthly 105, 446, 1998.
Schröder, E. ``Vier combinatorische Probleme.'' Z. Math. Physik 15, 361-376, 1870.
Sloane, N. J. A. Sequence
A001003/M2898
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stanley, R. P. ``Hipparchus, Plutarch, Schröder, and Hough.'' Amer. Math. Monthly 104, 344-350, 1997.