|
|
|

A Fractal which can be constructed using String Rewriting by creating a matrix three times the size of the current matrix using the rules
Let ![]() be the number of black boxes,
be the number of black boxes, ![]() the length of a side of a white box, and
the length of a side of a white box, and ![]() the fractional Area of
black boxes after the
the fractional Area of
black boxes after the ![]() th iteration.
th iteration.
| (1) | |||
| (2) | |||
| (3) |
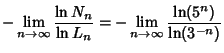 |
|||
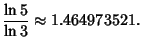 |
(4) |
See also Box Fractal, Sierpinski Carpet, Sierpinski Sieve
References
Dickau, R. M. ``Cantor Dust.''
http://forum.swarthmore.edu/advanced/robertd/cantor.html.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 103-104, 1993.
![]() Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.