|
|
|
Given
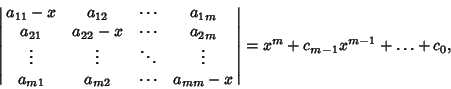 |
(1) |
| (2) |
 |
|||
| (3) |
![$\displaystyle \left[\begin{array}{cc}a & b\\ c & d\end{array}\right]$](c1_779.gif) |
(4) | ||
![$\displaystyle \left[\begin{array}{cc}a & b\\ c & d\end{array}\right]\left[\begin{array}{cc}a & b\\ c & d\end{array}\right]$](c1_781.gif) |
|||
![$\displaystyle \left[\begin{array}{cc}a^2+bc & ab+bd\\ ac+cd & bc+d^2\end{array}\right]$](c1_782.gif) |
(5) | ||
![$\displaystyle \left[\begin{array}{cc}-a^2-ad & -ab-bd\\ -ac-dc & -ad-d^2\end{array}\right]$](c1_784.gif) |
(6) | ||
![$\displaystyle \left[\begin{array}{cc}ad-bc & 0\\ 0 & ad-bc\end{array}\right],$](c1_786.gif) |
(7) |
| (8) |
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1117, 1979.
Segercrantz, J. ``Improving the Cayley-Hamilton Equation for Low-Rank Transformations.'' Amer. Math. Monthly
99, 42-44, 1992.