|
|
|
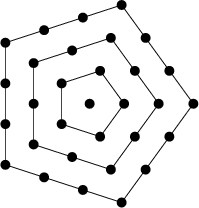
A Centered Polygonal Number consisting of a central dot with five dots around it, and then additional dots in the
gaps between adjacent dots. The general term is ![]() , and the first few such numbers are 1, 6, 16, 31, 51, 76,
... (Sloane's A005891). The Generating Function of the centered pentagonal numbers is
, and the first few such numbers are 1, 6, 16, 31, 51, 76,
... (Sloane's A005891). The Generating Function of the centered pentagonal numbers is
See also Centered Square Number, Centered Triangular Number
References
Sloane, N. J. A. Sequence
A005891/M4112
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.