|
|
|
The probability density function and cumulative distribution function are
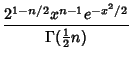 |
(1) | ||
| (2) |
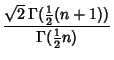 |
(3) | ||
![$\displaystyle {2[\Gamma({\textstyle{1\over 2}}n)\Gamma(1+{\textstyle{1\over 2}}n)-\Gamma^2({\textstyle{1\over 2}}(n+1))]\over\Gamma^2({\textstyle{1\over 2}}n)}$](c1_1483.gif) |
(4) | ||
![$\displaystyle {2\Gamma^3({\textstyle{1\over 2}}(n+1))-3\Gamma({\textstyle{1\ove...
...\Gamma(1+{\textstyle{1\over 2}}n)-\Gamma^2({\textstyle{1\over 2}}(n+1))]^{3/2}}$](c1_1484.gif) |
|||
![$\displaystyle +{\Gamma^2({\textstyle{1\over 2}}n)\Gamma({\textstyle{3+n\over 2}...
...\Gamma(1+{\textstyle{1\over 2}}n)-\Gamma^2({\textstyle{1\over 2}}(n+1))]^{3/2}}$](c1_1485.gif) |
(5) | ||
![$\displaystyle {-3\Gamma^4({\textstyle{1\over 2}}(n+1))+6\Gamma({\textstyle{1\ov...
...2}}n)\Gamma({\textstyle{2+n\over 2}})-\Gamma^2({\textstyle{1\over 2}}(n+1))]^2}$](c1_1486.gif) |
|||
![$\displaystyle +{-4\Gamma^2({\textstyle{1\over 2}}n)\Gamma({\textstyle{1\over 2}...
...}}n)\Gamma({\textstyle{2+n\over 2}})-\Gamma^2({\textstyle{1\over 2}}(n+1))]^2},$](c1_1487.gif) |
(6) |
where ![]() is the Mean,
is the Mean, ![]() the Variance,
the Variance, ![]() the Skewness, and
the Skewness, and ![]() the
Kurtosis. For
the
Kurtosis. For ![]() , the
, the ![]() distribution is a Half-Normal Distribution with
distribution is a Half-Normal Distribution with ![]() . For
. For ![]() , it
is a Rayleigh Distribution with
, it
is a Rayleigh Distribution with ![]() .
.
See also Chi-Squared Distribution, Half-Normal Distribution, Rayleigh Distribution