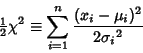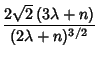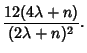A  distribution is a Gamma Distribution with
distribution is a Gamma Distribution with
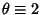 and
and
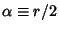 , where
, where  is the
number of Degrees of Freedom. If
is the
number of Degrees of Freedom. If 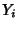 have Normal
Independent distributions with Mean 0 and Variance 1, then
have Normal
Independent distributions with Mean 0 and Variance 1, then
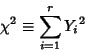 |
(1) |
is distributed as  with
with  Degrees of Freedom. If
Degrees of Freedom. If  are independently
distributed according to a
are independently
distributed according to a  distribution with
distribution with 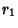 ,
, 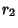 , ...,
, ..., 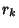 Degrees of Freedom, then
Degrees of Freedom, then
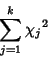 |
(2) |
is distributed according to  with
with
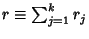 Degrees of Freedom.
Degrees of Freedom.
 |
(3) |
The cumulative distribution function is then
where 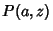 is a Regularized Gamma Function. The Confidence Intervals can be
found by finding the value of
is a Regularized Gamma Function. The Confidence Intervals can be
found by finding the value of  for which
for which 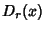 equals a given value. The Moment-Generating Function of the
equals a given value. The Moment-Generating Function of the
 distribution is
distribution is
so
The 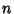 th Moment about zero for a distribution with
th Moment about zero for a distribution with  Degrees of Freedom is
Degrees of Freedom is
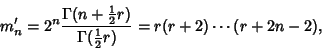 |
(13) |
and the moments about the Mean are
The 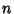 th Cumulant is
th Cumulant is
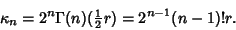 |
(17) |
The Moment-Generating Function is
As 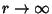 ,
,
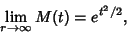 |
(19) |
so for large  ,
,
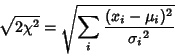 |
(20) |
is approximately a Gaussian Distribution with Mean 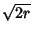 and Variance
and Variance 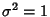 . Fisher
showed that
. Fisher
showed that
 |
(21) |
is an improved estimate for moderate  . Wilson and Hilferty showed that
. Wilson and Hilferty showed that
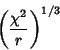 |
(22) |
is a nearly Gaussian Distribution with Mean  and Variance
and Variance
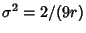 .
.
In a Gaussian Distribution,
 |
(23) |
let
 |
(24) |
Then
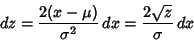 |
(25) |
so
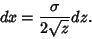 |
(26) |
But
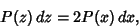 |
(27) |
so
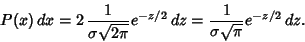 |
(28) |
This is a  distribution with
distribution with  , since
, since
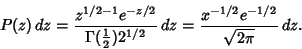 |
(29) |
If  are independent variates with a Normal Distribution having Means
are independent variates with a Normal Distribution having Means 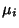 and
Variances
and
Variances 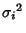 for
for 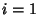 , ...,
, ..., 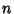 , then
, then
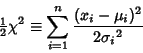 |
(30) |
is a Gamma Distribution variate with 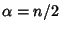 ,
,
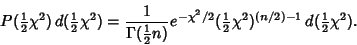 |
(31) |
The noncentral chi-squared distribution is given by
 |
(32) |
where
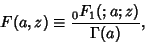 |
(33) |
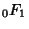 is the Confluent Hypergeometric Limit Function and
is the Confluent Hypergeometric Limit Function and  is the Gamma Function. The Mean,
Variance, Skewness, and Kurtosis are
is the Gamma Function. The Mean,
Variance, Skewness, and Kurtosis are
See also Chi Distribution, Snedecor's F-Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 940-943, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 535, 1987.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function.'' §6.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 209-214, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 115-116, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() distribution is a Gamma Distribution with
distribution is a Gamma Distribution with
![]() and
and
![]() , where
, where ![]() is the
number of Degrees of Freedom. If
is the
number of Degrees of Freedom. If ![]() have Normal
Independent distributions with Mean 0 and Variance 1, then
have Normal
Independent distributions with Mean 0 and Variance 1, then
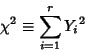



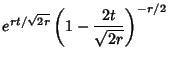
![$\displaystyle \left[{e^{t\sqrt{2/r}}\left({1-\sqrt{2\over r}\,t}\right)}\right]^{-r/2}$](c1_1529.gif)
![$\displaystyle \left[{1-{t^2\over r}-{1\over 3}\left({2\over r}\right)^{3/2}t^3-\ldots}\right]^{-r/2}.$](c1_1530.gif)
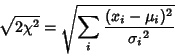
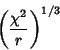
![]() are independent variates with a Normal Distribution having Means
are independent variates with a Normal Distribution having Means ![]() and
Variances
and
Variances ![]() for
for ![]() , ...,
, ..., ![]() , then
, then