|
|
|
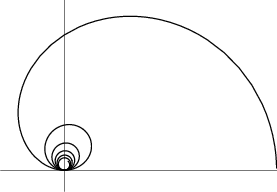
The cochleoid, whose name means ``snail-form'' in Latin, was first discussed by J. Peck in 1700 (MacTutor Archive). The points of contact of Parallel Tangents to the cochleoid lie on a Strophoid.
| (1) |
| (2) |
| (3) |
See also Quadratrix of Hippias
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 192 and 196, 1972.
MacTutor History of Mathematics Archive. ``Cochleoid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cochleoid.html.