|
|
|
Let ![]() be a curve, let
be a curve, let ![]() be a fixed point (the Pole), and let
be a fixed point (the Pole), and let ![]() be a second fixed point. Let
be a second fixed point. Let ![]() and
and ![]() be
points on a line through
be
points on a line through ![]() meeting
meeting ![]() at
at ![]() such that
such that
![]() . The Locus of
. The Locus of ![]() and
and ![]() is called the
strophoid of
is called the
strophoid of ![]() with respect to the Pole
with respect to the Pole ![]() and fixed point
and fixed point ![]() . Let
. Let ![]() be represented parametrically by
be represented parametrically by
![]() , and let
, and let ![]() and
and ![]() . Then the equation of the strophoid is
. Then the equation of the strophoid is
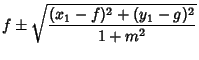 |
(1) | ||
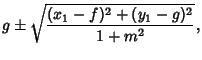 |
(2) |
| (3) |
| (4) |
| Curve | Pole | Fixed Point | Strophoid |
| line | not on line | on line | oblique strophoid |
| line | not on line | foot of Perpendicular origin to line | Right Strophoid |
| Circle | center | on the circumference | Freeth's Nephroid |
See also Right Strophoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 51-53 and 205, 1972.
Lockwood, E. H. ``Strophoids.'' Ch. 16 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 134-137, 1967.
MacTutor History of Mathematics Archive. ``Right.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Right.html.
Yates, R. C. ``Strophoid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 217-220, 1952.
|
|
|
© 1996-9 Eric W. Weisstein