|
|
|
A problem posed by L. Collatz in 1937, also called the 3x+1 Mapping, Hasse's Algorithm, Kakutani's
Problem, Syracuse Algorithm, Syracuse Problem, Thwaites Conjecture, and Ulam's Problem
(Lagarias 1985). Thwaites (1996) has offered a ![]() 1000 reward for resolving the Conjecture. Let
1000 reward for resolving the Conjecture. Let ![]() be an
Integer. Then the Collatz problem asks if iterating
be an
Integer. Then the Collatz problem asks if iterating
| (1) |
The Collatz problem was modified by Terras (1976, 1979), who asked if iterating
| (2) |
| (3) |
| (4) |
| (5) | |||
| (6) | |||
| (7) |
Conway proved that the original Collatz problem has no nontrivial cycles of length ![]() . Lagarias (1985) showed that
there are no nontrivial cycles with length
. Lagarias (1985) showed that
there are no nontrivial cycles with length ![]() . Conway (1972) also proved that Collatz-type problems can be
formally Undecidable.
. Conway (1972) also proved that Collatz-type problems can be
formally Undecidable.
A generalization of the Collatz Problem lets ![]() be a Positive Integer and
be a Positive Integer and ![]() , ...,
, ..., ![]() be Nonzero Integers. Also let
be Nonzero Integers. Also let ![]() satisfy
satisfy
| (8) |
| (9) |
| (10) |
| (11) |
| # Cycles | Max. Cycle Length | |
| 0 | 5 | 27 |
| 1 | 10 | 34 |
| 2 | 13 | 118 |
| 3 | 17 | 118 |
| 4 | 19 | 118 |
| 5 | 21 | 165 |
| 6 | 23 | 433 |
Matthews and Watts (1984) proposed the following conjectures.
|
|
|
|
|
(12) |
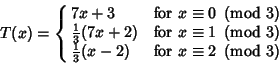 |
(13) |
See also Hailstone Number
References
Applegate, D. and Lagarias, J. C. ``Density Bounds for the
Applegate, D. and Lagarias, J. C. ``Density Bounds for the
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Burckel, S. ``Functional Equations Associated with Congruential Functions.'' Theor. Comp. Sci. 123, 397-406, 1994.
Conway, J. H. ``Unpredictable Iterations.'' Proc. 1972 Number Th. Conf., University of Colorado, Boulder, Colorado, pp. 49-52, 1972.
Crandall, R. ``On the `
Everett, C. ``Iteration of the Number Theoretic Function
Guy, R. K. ``Collatz's Sequence.'' §E16 in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 215-218, 1994.
Lagarias, J. C. ``The
Leavens, G. T. and Vermeulen, M. ``
Matthews, K. R. ``The Generalized
Matthews, K. R. ``A Generalized
Matthews, K. R. and Watts, A. M. ``A Generalization of Hasses's Generalization of the Syracuse Algorithm.''
Acta Arith. 43, 167-175, 1984.
Sloane, N. J. A. Sequence
A006667/M0019
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Terras, R. ``A Stopping Time Problem on the Positive Integers.'' Acta Arith. 30, 241-252, 1976.
Terras, R. ``On the Existence of a Density.'' Acta Arith. 35, 101-102, 1979.
Thwaites, B. ``Two Conjectures, or How to win
Vardi, I. ``The
![]() Problem 1. Tree-Search Method.''
Math. Comput. 64, 411-426, 1995.
Problem 1. Tree-Search Method.''
Math. Comput. 64, 411-426, 1995.
![]() Problem 2. Krasikov Inequalities.''
Math. Comput. 64, 427-438, 1995.
Problem 2. Krasikov Inequalities.''
Math. Comput. 64, 427-438, 1995.
![]() ' Problem.'' Math. Comput. 32, 1281-1292, 1978.
' Problem.'' Math. Comput. 32, 1281-1292, 1978.
![]() ,
,
![]() .'' Adv. Math. 25, 42-45, 1977.
.'' Adv. Math. 25, 42-45, 1977.
![]() Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985.
http://www.cecm.sfu.ca/organics/papers/lagarias/.
Problem and Its Generalizations.'' Amer. Math. Monthly 92, 3-23, 1985.
http://www.cecm.sfu.ca/organics/papers/lagarias/.
![]() Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992.
Search Programs.'' Comput. Math. Appl. 24, 79-99, 1992.
![]() Mapping.''
http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999.
Mapping.''
http://www.maths.uq.oz.au/~krm/survey.ps. Rev. Mar. 30, 1999.
![]() Conjecture.'' [$100 Reward for a Proof.]
ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge.
Conjecture.'' [$100 Reward for a Proof.]
ftp://www.maths.uq.edu.au/pub/krm/gnubc/challenge.
![]() 1100.'' Math.Gaz. 80, 35-36, 1996.
1100.'' Math.Gaz. 80, 35-36, 1996.
![]() Problem.'' Ch. 7 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.
Problem.'' Ch. 7 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, pp. 129-137, 1991.
|
|
|
© 1996-9 Eric W. Weisstein