Cyclide

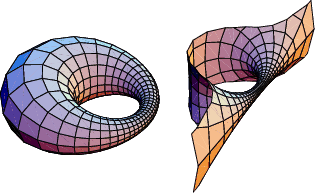
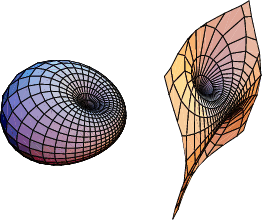
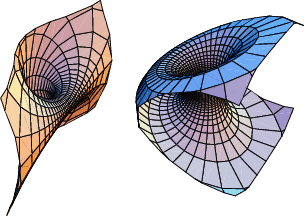
A pair of focal conics which are the envelopes of two one-parameter families of spheres, sometimes also called a Cyclid. The cyclide is a Quartic Surface, and the lines of curvature on a cyclide are all straight lines or circular arcs (Pinkall 1986). The Standard Tori and their inversions in a Sphere $S$ centered at a point ${\bf x}_0$ and of Radius $r$, given by

$$I({\bf x}_0, r)={\bf x}_0+{{\bf x}-{\bf x}_0r^2\over \vert{\bf x}-{\bf x}_0\vert^2},$$

are both cyclides (Pinkall 1986). Illustrated above are Ring Cyclides, Horn Cyclides, and Spindle Cyclides. The figures on the right correspond to ${\bf x}_0$ lying on the torus itself, and are called the Parabolic Ring Cyclide, Parabolic Horn Cyclide, and Parabolic Spindle Cyclide, respectively.

See also Cyclidic Coordinates, Horn Cyclide, Parabolic Horn Cyclide, Parabolic Ring Cyclide, Ring Cyclide, Spindle Cyclide, Standard Tori

References

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, p. 273, 1959.

Eisenhart, L. P. ``Cyclides of Dupin.'' §133 in A Treatise on the Differential Geometry of Curves and Surfaces. New York: Dover, pp. 312-314, 1960.

Fischer, G. (Ed.). Plates 71-77 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, pp. 66-72, 1986.

Nordstrand, T. ``Dupin Cyclide.'' http://www.uib.no/people/nfytn/dupintxt.htm.

Pinkall, U. ``Cyclides of Dupin.'' §3.3 in Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 28-30, 1986.

Salmon, G. Analytic Geometry of Three Dimensions. New York: Chelsea, p. 527, 1979.