|
|
|
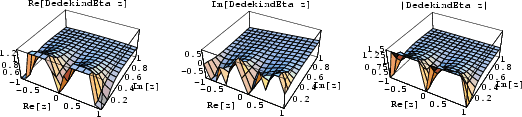
Let
| (1) |
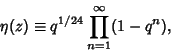 |
(2) |
![\begin{displaymath}
\eta(z)=q^{1/24}\left\{{1+\sum_{n=1}^\infty (-1)^n [q^{n(3n-1)/2}+q^{n(3n+1)/2}]}\right\}
\end{displaymath}](d1_344.gif) |
(3) |
| (4) | |||
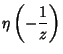 |
(5) |
See also Dirichlet Eta Function, Theta Function, Weber Functions
References
Atkin, A. O. L. and Morain, F. ``Elliptic Curves and Primality Proving.'' Math. Comput. 61, 29-68, 1993.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1902.