|
|
|
A function ![]() is said to be an entire modular form of weight
is said to be an entire modular form of weight ![]() if it satisfies
if it satisfies
![$\left[{\matrix{a & b\cr c & d\cr}}\right]$](m_1466.gif) is a member of the
Modular group
is a member of the
Modular group 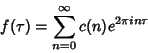
A remarkable connection between rational Elliptic Curves and modular forms is given by the Taniyama-Shimura Conjecture, which states that any rational Elliptic Curve is a modular form in disguise. This result was the one proved by Andrew Wiles in his celebrated proof of Fermat's Last Theorem.
See also Cusp Form, Elliptic Curve, Elliptic Function, Fermat's Last Theorem, Hecke Algebra, Modular Function, Modular Function Multiplier, Schläfli's Modular Form, Taniyama-Shimura Conjecture
References
Apostol, T. M. ``Modular Forms with Multiplicative Coefficients.'' Ch. 6 in
Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 113-141, 1997.
Knopp, M. I. Modular Functions, 2nd ed. New York: Chelsea, 1993.
Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.
Sarnack, P. Some Applications of Modular Forms. Cambridge, England: Cambridge University Press, 1993.