|
|
|
A function is said to be modular (or ``elliptic modular'') if it satisfies:
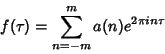
An important property of modular functions is that if ![]() is modular and not identically 0, then the number of zeros of
is modular and not identically 0, then the number of zeros of ![]() is
equal to the number of poles of
is
equal to the number of poles of ![]() in the Closure of the fundamental region
in the Closure of the fundamental region ![]() (Apostol 1997, p. 34).
(Apostol 1997, p. 34).
See also Elliptic Function, Modular Form
References
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory. New York: Springer-Verlag, 1976.
Borwein, J. M. and Borwein, P. B. Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.
Schoeneberg, B. Elliptic Modular Functions: An Introduction. Berlin: New York: Springer-Verlag, 1974.
![]() Modular Functions
Modular Functions