The modular equation of degree 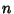 gives an algebraic connection of the form
gives an algebraic connection of the form
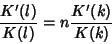 |
(1) |
between the Transcendental Complete Elliptic Integrals of the First
Kind with moduli 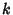 and
and  . When
. When 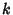 and
and  satisfy a modular equation, a
relationship of the form
satisfy a modular equation, a
relationship of the form
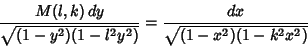 |
(2) |
exists, and 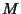 is called the Modular Function Multiplier. In general, if
is called the Modular Function Multiplier. In general, if 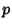 is an Odd Prime, then the
modular equation is given by
is an Odd Prime, then the
modular equation is given by
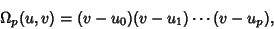 |
(3) |
where
![\begin{displaymath}
u_p\equiv (-1)^{(p^2-1)/8}[\lambda(q^p)]^{1/8}\equiv (-1)^{(p^2-1)/8}u(q^p),
\end{displaymath}](m_1438.gif) |
(4) |
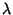 is a Elliptic Lambda Function, and
is a Elliptic Lambda Function, and
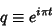 |
(5) |
(Borwein and Borwein 1987, p. 126). An Elliptic Integral identity gives
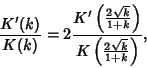 |
(6) |
so the modular equation of degree 2 is
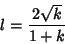 |
(7) |
which can be written as
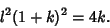 |
(8) |
A few low order modular equations written in terms of 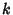 and
and  are
In terms of
are
In terms of  and
and 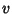 ,
,
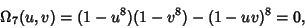 |
(14) |
where
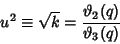 |
(15) |
and
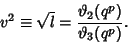 |
(16) |
Here, 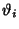 are Theta Functions.
are Theta Functions.
A modular equation of degree 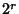 for
for 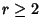 can be obtained by iterating the equation for
can be obtained by iterating the equation for 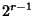 . Modular equations
for Prime
. Modular equations
for Prime 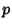 from 3 to 23 are given in Borwein and Borwein (1987).
from 3 to 23 are given in Borwein and Borwein (1987).
Quadratic modular identities include
![\begin{displaymath}
{\vartheta _3(q)\over \vartheta _3(q^4)}-1=\left[{{{\vartheta _3}^2(q^2)\over {\vartheta _3}^2(q^4)}-1}\right]^{1/2}.
\end{displaymath}](m_1458.gif) |
(17) |
Cubic identities include
![\begin{displaymath}
\left[{3 {\vartheta _2(q^9)\over \vartheta _2(q)}-1}\right]^3=9{{\vartheta _2}^4(q^3)\over {\vartheta _2}^4(q)}-1
\end{displaymath}](m_1459.gif) |
(18) |
![\begin{displaymath}
\left[{3 {\vartheta _3(q^9)\over \vartheta _3(q)}-1}\right]^3=9{{\vartheta _3}^4(q^3)\over {\vartheta _3}^4(q)}-1
\end{displaymath}](m_1460.gif) |
(19) |
![\begin{displaymath}
\left[{3 {\vartheta _4(q^9)\over \vartheta _4(q)}-1}\right]^3=9{{\vartheta _4}^4(q^3)\over {\vartheta _4}^4(q)}-1.
\end{displaymath}](m_1461.gif) |
(20) |
A seventh-order identity is
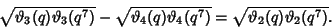 |
(21) |
From Ramanujan (1913-1914),
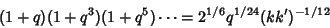 |
(22) |
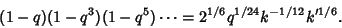 |
(23) |
See also Schläfli's Modular Form
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 127-132, 1987.
Hanna, M. ``The Modular Equations.'' Proc. London Math. Soc. 28, 46-52, 1928.
Ramanujan, S. ``Modular Equations and Approximations to 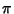 .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() gives an algebraic connection of the form
gives an algebraic connection of the form
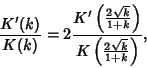
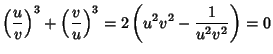
![]() for
for ![]() can be obtained by iterating the equation for
can be obtained by iterating the equation for ![]() . Modular equations
for Prime
. Modular equations
for Prime ![]() from 3 to 23 are given in Borwein and Borwein (1987).
from 3 to 23 are given in Borwein and Borwein (1987).
![\begin{displaymath}
{\vartheta _3(q)\over \vartheta _3(q^4)}-1=\left[{{{\vartheta _3}^2(q^2)\over {\vartheta _3}^2(q^4)}-1}\right]^{1/2}.
\end{displaymath}](m_1458.gif)
![\begin{displaymath}
\left[{3 {\vartheta _2(q^9)\over \vartheta _2(q)}-1}\right]^3=9{{\vartheta _2}^4(q^3)\over {\vartheta _2}^4(q)}-1
\end{displaymath}](m_1459.gif)
![\begin{displaymath}
\left[{3 {\vartheta _3(q^9)\over \vartheta _3(q)}-1}\right]^3=9{{\vartheta _3}^4(q^3)\over {\vartheta _3}^4(q)}-1
\end{displaymath}](m_1460.gif)
![\begin{displaymath}
\left[{3 {\vartheta _4(q^9)\over \vartheta _4(q)}-1}\right]^3=9{{\vartheta _4}^4(q^3)\over {\vartheta _4}^4(q)}-1.
\end{displaymath}](m_1461.gif)
![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.