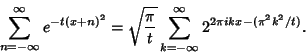The theta functions are the elliptic analogs of the Exponential Function, and may be used to express the Jacobi Elliptic
Functions. Let 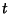 be a constant Complex Number with
be a constant Complex Number with ![$\Im[t]> 0$](t_522.gif) . Define the Nome
. Define the Nome
 |
(1) |
where
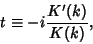 |
(2) |
and  is a complete Elliptic Integral of the First Kind,
is a complete Elliptic Integral of the First Kind, 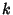 is the Modulus, and
is the Modulus, and 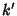 is the complementary Modulus. Then the theta functions are, in
the Notation of Whittaker and Watson,
is the complementary Modulus. Then the theta functions are, in
the Notation of Whittaker and Watson,
Written in terms of 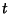 ,
,
These functions are sometimes denoted 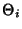 or
or 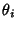 , and a number of indexing conventions have been used. For a
summary of these notations, see Whittaker and Watson (1990). The theta functions are quasidoubly periodic, as illustrated
in the following table.
, and a number of indexing conventions have been used. For a
summary of these notations, see Whittaker and Watson (1990). The theta functions are quasidoubly periodic, as illustrated
in the following table.
Here,
 |
(9) |
The quasiperiodicity can be established as follows for the specific case of 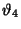 ,
,
The theta functions can be written in terms of each other:
Any theta function of given arguments can be expressed in terms of any other two theta functions with the same arguments.
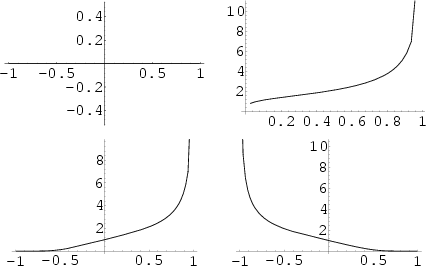
Define
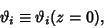 |
(15) |
which are plotted above. Then we have the identities
 |
(16) |
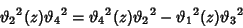 |
(17) |
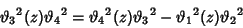 |
(18) |
 |
(19) |
Taking 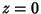 in the last gives the special case
in the last gives the special case
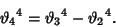 |
(20) |
In addition,
The theta functions obey addition rules such as
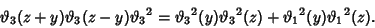 |
(25) |
Letting  gives a duplication Formula
gives a duplication Formula
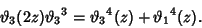 |
(26) |
For more addition Formulas, see Whittaker and Watson (1990, pp. 487-488). Ratios of theta function
derivatives to the functions themselves have the simple forms
The theta functions can be expressed as products instead of sums by
where
 |
(35) |
(Whittaker and Watson 1990, pp. 469-470).
The theta functions satisfy the Partial Differential Equation
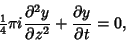 |
(36) |
where
 . Ratios of the theta functions with
. Ratios of the theta functions with 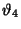 in the Denominator also satisfy
differential equations
in the Denominator also satisfy
differential equations
 |
(37) |
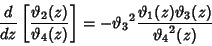 |
(38) |
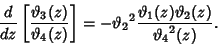 |
(39) |
Some additional remarkable identities are
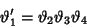 |
(40) |
 |
(41) |
which were discovered by Poisson  in 1827 and are equivalent to
in 1827 and are equivalent to
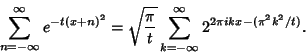 |
(42) |
Another amazing identity is
(Whittaker and Watson 1990, p. 469).
The complete Elliptic Integrals of the First and Second
Kinds can be expressed using theta functions. Let
 |
(44) |
and plug into (37)
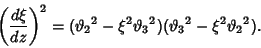 |
(45) |
Now write
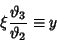 |
(46) |
and
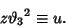 |
(47) |
Then
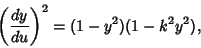 |
(48) |
where the Modulus is defined by
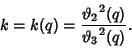 |
(49) |
Define also the complementary Modulus
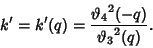 |
(50) |
Now, since
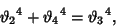 |
(51) |
we have shown
 |
(52) |
The solution to the equation is
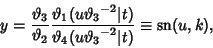 |
(53) |
which is a Jacobi Elliptic Function with periods
 |
(54) |
and
 |
(55) |
Here,  is the complete Elliptic Integral of the First Kind,
is the complete Elliptic Integral of the First Kind,
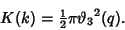 |
(56) |
See also Blecksmith-Brillhart-Gerst Theorem, Elliptic Function, Eta Function, Euler's Pentagonal
Number Theorem, Jacobi Elliptic Functions, Jacobi Triple Product, Landen's Formula, Mock Theta
Function, Modular Equation, Modular Transformation, Mordell Integral, Neville Theta Function,
Nome, Poincaré-Fuchs-Klein Automorphic Function,
Prime Theta Function,
Quintuple Product Identity, Ramanujan Theta Functions, Schröter's Formula,
Weber Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 577, 1972.
Bellman, R. E. A Brief Introduction to Theta Functions. New York: Holt, Rinehart and Winston, 1961.
Berndt, B. C. ``Theta-Functions and Modular Equations.'' Ch. 25 in Ramanujan's Notebooks, Part IV.
New York: Springer-Verlag, pp. 138-244, 1994.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 430-432, 1953.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be a constant Complex Number with
be a constant Complex Number with ![]() . Define the Nome
. Define the Nome
![$\displaystyle 2 \sum_{n=0}^\infty (-1)^n q^{(n+1/2)^2}\sin [(2n+1)z]$](t_528.gif)
![$\displaystyle z q^{1/4} \sum_{n=0}^\infty (-1)^n q^{n(n+1)}\sin[(2n+1)z]$](t_529.gif)
![$\displaystyle 2\sum_{n=0}^\infty q^{(n+1/2)^2}\cos[(2n+1)z]$](t_531.gif)
![$\displaystyle 2q^{1/4} \sum_{n=0}^\infty q^{n(n+1)}\cos[(2n+1)z]$](t_532.gif)
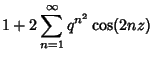
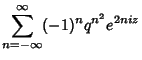
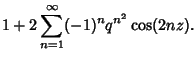
![$\displaystyle \sum_{n=-\infty}^\infty q^{(n+1/2)^2}e^{\Im[t]}$](t_539.gif)
![$\displaystyle \sum_{n=-\infty}^\infty q^{n^2} e^{\Im[t]}.$](t_541.gif)
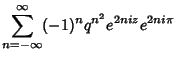
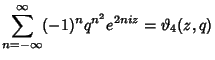
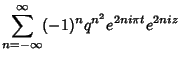


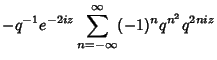
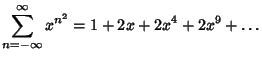

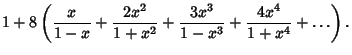
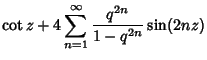
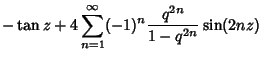
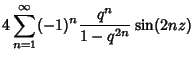
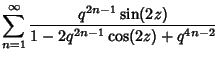
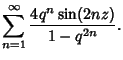
![$\displaystyle 2Gq^{1/4}\sin z \prod_{n=1}^\infty [1-2q^{2n} \cos(2z)+q^{4n}]$](t_593.gif)
![$\displaystyle 2Gq^{1/4}\cos z \prod_{n=1}^\infty [1+2q^{2n} \cos(2z)+q^{4n}]$](t_595.gif)
![$\displaystyle G \prod_{n=1}^\infty [1+2q^{2n-1}\cos(2z)+q^{4n-2}]$](t_597.gif)
![$\displaystyle G \prod_{n=1}^\infty [1-2q^{2n-1}\cos(2z)+q^{4n-2}],$](t_599.gif)