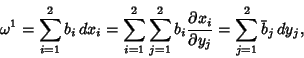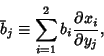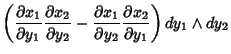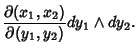A differential  -form is a Tensor of Rank
-form is a Tensor of Rank  which is antisymmetric under exchange of any
pair of indices. The number of algebraically independent components in
which is antisymmetric under exchange of any
pair of indices. The number of algebraically independent components in  -D is
-D is 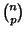 , where this is a
Binomial Coefficient. In particular, a 1-form (often simply called a ``differential'') is a quantity
, where this is a
Binomial Coefficient. In particular, a 1-form (often simply called a ``differential'') is a quantity
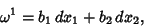 |
(1) |
where
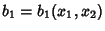 and
and
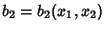 are the components of a Covariant Tensor. Changing variables from
are the components of a Covariant Tensor. Changing variables from
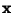 to
to 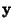 gives
gives
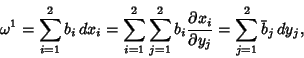 |
(2) |
where
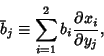 |
(3) |
which is the covariant transformation law. 2-forms can be constructed from the Wedge Product of 1-forms. Let
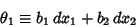 |
(4) |
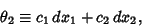 |
(5) |
then
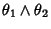 is a 2-form denoted
is a 2-form denoted 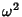 . Changing variables
. Changing variables 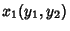 to
to  gives
gives
 |
(6) |
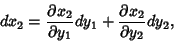 |
(7) |
so
Similarly, a 4-form can be constructed from Wedge Products of two 2-forms or four 1-forms
 |
(9) |
See also Angle Bracket, Bra, Exterior Derivative, Ket, One-Form, Symplectic Form,
Wedge Product
References
Weintraub, S. H. Differential Forms: A Complement to Vector Calculus. San Diego, CA:
Academic Press, 1996.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() -form is a Tensor of Rank
-form is a Tensor of Rank ![]() which is antisymmetric under exchange of any
pair of indices. The number of algebraically independent components in
which is antisymmetric under exchange of any
pair of indices. The number of algebraically independent components in ![]() -D is
-D is ![]() , where this is a
Binomial Coefficient. In particular, a 1-form (often simply called a ``differential'') is a quantity
, where this is a
Binomial Coefficient. In particular, a 1-form (often simply called a ``differential'') is a quantity