In order to find Integers  and
and  such that
such that
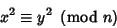 |
(1) |
(a modified form of Fermat's Factorization Method), in which case there is a 50% chance that
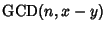 is a
Factor of
is a
Factor of 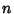 , choose a Random Integer
, choose a Random Integer 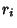 , compute
, compute
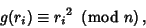 |
(2) |
and try to factor 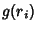 . If
. If 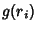 is not easily factorable (up to some small trial divisor
is not easily factorable (up to some small trial divisor 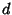 ), try another
), try another
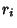 . In practice, the trial
. In practice, the trial 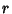 s are usually taken to be
s are usually taken to be
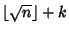 , with
, with  , 2, ..., which
allows the Quadratic Sieve Factorization Method to be used. Continue finding and factoring
, 2, ..., which
allows the Quadratic Sieve Factorization Method to be used. Continue finding and factoring 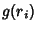 s until
s until
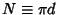 are found, where
are found, where 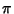 is the Prime Counting Function. Now for each
is the Prime Counting Function. Now for each 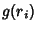 , write
, write
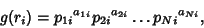 |
(3) |
and form the Exponent Vector
![\begin{displaymath}
{\bf v}(r_i)=\left[{\matrix{a_{1i}\cr a_{2i}\cr \vdots\cr a_{Ni}\cr}}\right].
\end{displaymath}](d2_1318.gif) |
(4) |
Now, if  are even for any
are even for any  , then
, then 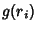 is a Square Number and we have found a solution to (1).
If not, look for a linear combination
is a Square Number and we have found a solution to (1).
If not, look for a linear combination
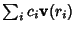 such that the elements are all even, i.e.,
such that the elements are all even, i.e.,
![\begin{displaymath}
c_1\left[{\matrix{a_{11}\cr a_{21}\cr \vdots\cr a_{N1}\cr}}\...
...matrix{0\cr 0\cr \vdots\cr 0\cr}}\right] \quad ({\rm mod\ } 2)
\end{displaymath}](d2_1321.gif) |
(5) |
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1N}\cr
a_{21} ...
...atrix{0\cr 0\cr \vdots\cr 0\cr}}\right] \quad ({\rm mod\ } 2).
\end{displaymath}](d2_1322.gif) |
(6) |
Since this must be solved only mod 2, the problem can be simplified by replacing the 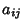 s with
s with
 |
(7) |
Gaussian Elimination can then be used to solve
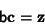 |
(8) |
for 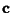 , where
, where 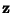 is a Vector equal to
is a Vector equal to  (mod 2). Once
(mod 2). Once 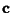 is known, then we have
is known, then we have
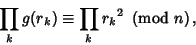 |
(9) |
where the products are taken over all  for which
for which 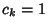 . Both sides are Perfect Squares, so we have a 50%
chance that this yields a nontrivial factor of
. Both sides are Perfect Squares, so we have a 50%
chance that this yields a nontrivial factor of 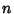 . If it does not, then we proceed to a different
. If it does not, then we proceed to a different 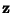 and repeat
the procedure. There is no guarantee that this method will yield a factor, but in practice it produces factors faster than
any method using trial divisors. It is especially amenable to parallel processing, since each processor can work on a
different value of
and repeat
the procedure. There is no guarantee that this method will yield a factor, but in practice it produces factors faster than
any method using trial divisors. It is especially amenable to parallel processing, since each processor can work on a
different value of 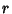 .
.
References
Bressoud, D. M. Factorization and Prime Testing. New York: Springer-Verlag, pp. 102-104, 1989.
Dixon, J. D. ``Asymptotically Fast Factorization of Integers.'' Math. Comput. 36, 255-260, 1981.
Lenstra, A. K. and Lenstra, H. W. Jr. ``Algorithms in Number Theory.'' In
Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity (Ed. J. van Leeuwen).
New York: Elsevier, pp. 673-715, 1990.
Pomerance, C. ``A Tale of Two Sieves.'' Not. Amer. Math. Soc. 43, 1473-1485, 1996.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() and
and ![]() such that
such that
![\begin{displaymath}
{\bf v}(r_i)=\left[{\matrix{a_{1i}\cr a_{2i}\cr \vdots\cr a_{Ni}\cr}}\right].
\end{displaymath}](d2_1318.gif)
![\begin{displaymath}
c_1\left[{\matrix{a_{11}\cr a_{21}\cr \vdots\cr a_{N1}\cr}}\...
...matrix{0\cr 0\cr \vdots\cr 0\cr}}\right] \quad ({\rm mod\ } 2)
\end{displaymath}](d2_1321.gif)
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1N}\cr
a_{21} ...
...atrix{0\cr 0\cr \vdots\cr 0\cr}}\right] \quad ({\rm mod\ } 2).
\end{displaymath}](d2_1322.gif)