Dodecahedron-Icosahedron Compound

$\begin{figure}\BoxedEPSF{DodecahedronIcos_net.epsf scaled 400}\end{figure}$

A Polyhedron Compound of a Dodecahedron and Icosahedron which is most easily constructed by adding 20 triangular Pyramids, constructed as above, to an Icosahedron. In the compound, the Dodecahedron and Icosahedron are rotated $\pi/5$ radians with respect to each other, and the ratio of the Icosahedron to Dodecahedron edges lengths are the Golden Ratio $\phi$ .

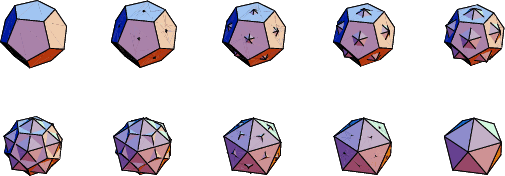
$\begin{figure}\begin{center}\BoxedEPSF{DodecIcosSeries.epsf scaled 700}\end{center}\end{figure}$

The above figure shows compounds composed of a Dodecahedron of unit edge length and Icosahedra having edge lengths varying from $\sqrt{5}/2$ (inscribed in the dodecahedron) to 2 (circumscribed about the dodecahedron).

The intersecting edges of the compound form the Diagonals of 30 Rhombuses comprising the Triacontahedron, which is the Dual Polyhedron of the Icosidodecahedron (Ball and Coxeter 1987). The dodecahedron-icosahedron is the first Stellation of the Icosidodecahedron.

References

Cundy, H. and Rollett, A. Mathematical Models, 2nd ed. Stradbroke, England: Tarquin Pub., p. 131, 1989.

Wenninger, M. J. Polyhedron Models. Cambridge, England: Cambridge University Press, p. 76, 1989.