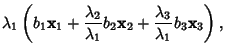A right eigenvector satisfies
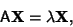 |
(1) |
where 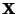 is a column Vector. The right Eigenvalues therefore satisfy
is a column Vector. The right Eigenvalues therefore satisfy
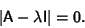 |
(2) |
A left eigenvector satisfies
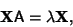 |
(3) |
where 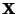 is a row Vector, so
is a row Vector, so
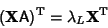 |
(4) |
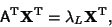 |
(5) |
where
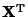 is the transpose of
is the transpose of 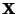 .
The left Eigenvalues satisfy
.
The left Eigenvalues satisfy
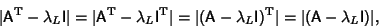 |
(6) |
(since
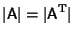 ) where
) where
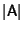 is the Determinant
of A. But this is the same equation satisfied by the
right Eigenvalues, so the left and right Eigenvalues are the same. Let
is the Determinant
of A. But this is the same equation satisfied by the
right Eigenvalues, so the left and right Eigenvalues are the same. Let 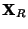 be a Matrix formed by the columns of the right eigenvectors and
be a Matrix formed by the columns of the right eigenvectors and 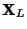 be a Matrix formed by the
rows of the left eigenvectors. Let
be a Matrix formed by the
rows of the left eigenvectors. Let
![\begin{displaymath}
{\hbox{\sf D}}\equiv \left[{\matrix{\lambda_1 & \cdots & 0\cr \vdots & \ddots & \vdots\cr 0 & \cdots & \lambda_n}}\right].
\end{displaymath}](e_263.gif) |
(7) |
Then
 |
(8) |
 |
(9) |
so
 |
(10) |
But this equation is of the form
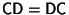 where
where
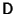 is a Diagonal Matrix, so it must be true
that
is a Diagonal Matrix, so it must be true
that
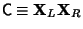 is also diagonal. In particular, if A is a Symmetric Matrix, then the
left and right eigenvectors are transposes of each other. If A is a Self-Adjoint Matrix, then the left and
right eigenvectors are conjugate Hermitian Matrices.
is also diagonal. In particular, if A is a Symmetric Matrix, then the
left and right eigenvectors are transposes of each other. If A is a Self-Adjoint Matrix, then the left and
right eigenvectors are conjugate Hermitian Matrices.
Given a 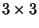 Matrix A with eigenvectors
Matrix A with eigenvectors 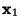 ,
, 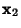 , and
, and 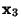 and corresponding
Eigenvalues
and corresponding
Eigenvalues  ,
, 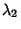 , and
, and 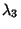 , then an arbitrary Vector
, then an arbitrary Vector  can be written
can be written
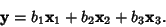 |
(11) |
Applying the Matrix A,
so
![\begin{displaymath}
{\hbox{\sf A}}^n{\bf y}={\lambda_1}^n \left[{b_1{\bf x_1}+\l...
...\left({\lambda_3\over\lambda_1}\right)^n b_3{\bf x}_3}\right].
\end{displaymath}](e_281.gif) |
(13) |
If
 , it therefore follows that
, it therefore follows that
 |
(14) |
so repeated application of the matrix to an arbitrary vector results in a vector proportional to the Eigenvector
having the largest Eigenvalue.
See also Eigenfunction, Eigenvalue
References
Arfken, G. ``Eigenvectors, Eigenvalues.'' §4.7 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 229-237, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Eigensystems.'' Ch. 11 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 449-489, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![\begin{displaymath}
{\hbox{\sf D}}\equiv \left[{\matrix{\lambda_1 & \cdots & 0\cr \vdots & \ddots & \vdots\cr 0 & \cdots & \lambda_n}}\right].
\end{displaymath}](e_263.gif)
![]() Matrix A with eigenvectors
Matrix A with eigenvectors ![]() ,
, ![]() , and
, and ![]() and corresponding
Eigenvalues
and corresponding
Eigenvalues ![]() ,
, ![]() , and
, and ![]() , then an arbitrary Vector
, then an arbitrary Vector ![]() can be written
can be written