Consider the family of Ellipses
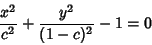 |
(1) |
for ![$c\in [0,1]$](e_611.gif) . The Partial Derivative with respect to
. The Partial Derivative with respect to  is
is
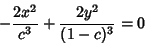 |
(2) |
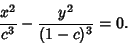 |
(3) |
Combining (1) and (3) gives the set of equations
![\begin{displaymath}
\left[{\matrix{{1\over c^2} & {1\over(1-c)^2}\cr
{1\over c^3...
...rix{x^2\cr y^2\cr}}\right] = \left[{\matrix{1\cr 0\cr}}\right]
\end{displaymath}](e_614.gif) |
(4) |
where the Discriminant is
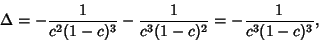 |
(6) |
so (5) becomes
![\begin{displaymath}
\left[{\matrix{x^2\cr y^2\cr}}\right]=\left[{\matrix{c^3\cr (1-c)^3\cr}}\right].
\end{displaymath}](e_619.gif) |
(7) |
Eliminating  then gives
then gives
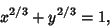 |
(8) |
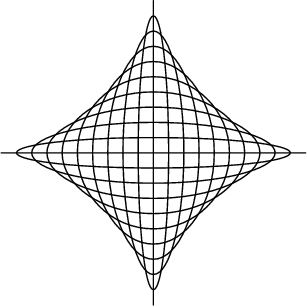
which is the equation of the Astroid.
If the curve is instead represented parametrically, then
Solving
![${\partial x\over\partial t}{\partial y\over\partial c}-{\partial x\over\partial c}{\partial y\over\partial t} = (-c\sin t)(-\sin t)-(\cos t)[(1-c)\cos t]$](e_623.gif)
|
|
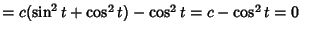
|
(11) |
for  gives
gives
 |
(12) |
so substituting this back into (9) and (10) gives
the parametric equations of the Astroid.
See also Astroid, Ellipse, Envelope
© 1996-9 Eric W. Weisstein
1999-05-25
![$\displaystyle {1\over\Delta}\left[\begin{array}{cc} -{1\over(1-c)^3} & -{1\over...
... & {1\over c^2}\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]$](e_616.gif)
![$\displaystyle {1\over\Delta}\left[\begin{array}{c}-{1\over(1-c)^3}\\ -{1\over c^3}\end{array}\right],$](e_617.gif)