Given a system of periodic Ordinary Differential Equations of the form
![\begin{displaymath}
{d\over dt} \left[{\matrix{x\cr y\cr v_x\cr v_y\cr}}\right] ...
... 0\cr}}\right]\left[{\matrix{x\cr y\cr v_x\cr v_y\cr}}\right],
\end{displaymath}](f_1477.gif) |
(1) |
the solution can be written as a linear combination of functions of the form
![\begin{displaymath}
\left[{\matrix{x(t)\cr y(t)\cr v_x(t)\cr v_y(t)\cr}}\right] ...
...x{x_0\cr y_0\cr v_{x0}\cr v_{y0}\cr}}\right]e^{\mu t}P_\mu(t),
\end{displaymath}](f_1478.gif) |
(2) |
where  is a function periodic with the same period
is a function periodic with the same period 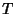 as the equations themselves. Given an Ordinary
Differential Equation of the form
as the equations themselves. Given an Ordinary
Differential Equation of the form
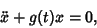 |
(3) |
where  is periodic with period
is periodic with period 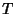 , the ODE has a pair of independent solutions given by the
Real and Imaginary Parts of
, the ODE has a pair of independent solutions given by the
Real and Imaginary Parts of
Plugging these into (3) gives
 |
(7) |
so the Real and Imaginary Parts are
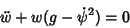 |
(8) |
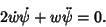 |
(9) |
From (9),
Integrating gives
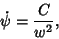 |
(11) |
where 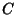 is a constant which must equal 1, so
is a constant which must equal 1, so 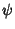 is given by
is given by
 |
(12) |
The Real solution is then
![\begin{displaymath}
x(t)=w(t)\cos[\psi(t)],
\end{displaymath}](f_1498.gif) |
(13) |
so
and
which is an integral of motion. Therefore, although 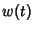 is not explicitly known, an integral
is not explicitly known, an integral 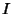 always exists.
Plugging (10) into (8) gives
always exists.
Plugging (10) into (8) gives
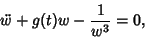 |
(16) |
which, however, is not any easier to solve than (3).
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 727, 1972.
Binney, J. and Tremaine, S. Galactic Dynamics. Princeton, NJ: Princeton University Press, p. 175, 1987.
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, p. 32, 1983.
Margenau, H. and Murphy, G. M. The Mathematics of Physics and Chemistry, 2 vols.
Princeton, NJ: Van Nostrand, 1956-64.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 556-557, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
{d\over dt} \left[{\matrix{x\cr y\cr v_x\cr v_y\cr}}\right] ...
... 0\cr}}\right]\left[{\matrix{x\cr y\cr v_x\cr v_y\cr}}\right],
\end{displaymath}](f_1477.gif)
![\begin{displaymath}
\left[{\matrix{x(t)\cr y(t)\cr v_x(t)\cr v_y(t)\cr}}\right] ...
...x{x_0\cr y_0\cr v_{x0}\cr v_{y0}\cr}}\right]e^{\mu t}P_\mu(t),
\end{displaymath}](f_1478.gif)
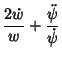
![$\displaystyle 2 {d\over dt} (\ln w)+{d\over dt} [\ln(\dot\psi)]$](f_1493.gif)
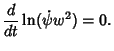
![$\displaystyle \cos ^2\psi+\sin ^2\psi=x^2w^{-2}+\left[{w\left({\dot w {x\over w}-\dot x}\right)}\right]^2$](f_1501.gif)