A quantitative measure of the simplicity of a Geometric Construction which reduces geometric constructions to
five steps. It was devised by È. Lemoine.
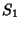 Place a Straightedge's Edge through a given Point,
Place a Straightedge's Edge through a given Point,
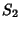 Draw a straight Line,
Draw a straight Line,
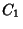 Place a Point of a Compass on a given Point,
Place a Point of a Compass on a given Point,
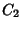 Place a Point of a Compass on an indeterminate Point on a Line,
Place a Point of a Compass on an indeterminate Point on a Line,
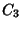 Draw a Circle.
Draw a Circle.
Geometrography seeks to reduce the number of operations (called the ``Simplicity'') needed to effect a construction.
If the number of the above operations are denoted 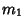 ,
,  ,
, 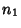 ,
, 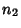 , and
, and 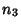 , respectively, then the
Simplicity is
, respectively, then the
Simplicity is
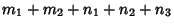 and the symbol is
and the symbol is
 .
It is apparently an unsolved problem to determine if a given Geometric
Construction is of the smallest possible simplicity.
.
It is apparently an unsolved problem to determine if a given Geometric
Construction is of the smallest possible simplicity.
See also Simplicity
References
De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly
98, 97-108, 1991.
Eves, H. An Introduction to the History of Mathematics, 6th ed. New York: Holt, Rinehart, and Winston, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25