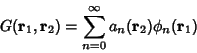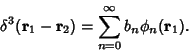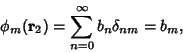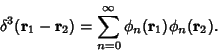Let
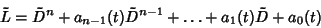 |
(1) |
be a differential Operator in 1-D, with 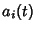 Continuous for
Continuous for 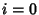 , 1, ...,
, 1, ...,
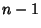 on the interval
on the interval 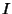 , and assume we wish to find the solution
, and assume we wish to find the solution 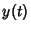 to the equation
to the equation
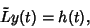 |
(2) |
where  is a given Continuous on
is a given Continuous on 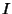 . To solve equation (2), we look for a function
. To solve equation (2), we look for a function
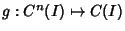 such that
such that
 , where
, where
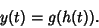 |
(3) |
This is a Convolution equation of the form
 |
(4) |
so the solution is
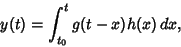 |
(5) |
where the function 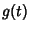 is called the Green's function for
is called the Green's function for 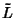 on
on 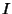 .
.
Now, note that if we take
 , then
, then
 |
(6) |
so the Green's function can be defined by
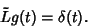 |
(7) |
However, the Green's function can be uniquely determined only if some initial or boundary conditions are given.
For an arbitrary linear differential operator 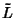 in 3-D, the Green's function
in 3-D, the Green's function
 is defined by
analogy with the 1-D case by
is defined by
analogy with the 1-D case by
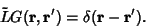 |
(8) |
The solution to
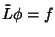 is then
is then
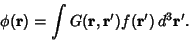 |
(9) |
Explicit expressions for
 can often be found in terms of a basis of given eigenfunctions
can often be found in terms of a basis of given eigenfunctions
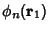 by expanding
the Green's function
by expanding
the Green's function
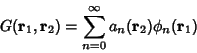 |
(10) |
and Delta Function,
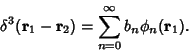 |
(11) |
Multiplying both sides by
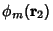 and integrating over
and integrating over  space,
space,
 |
(12) |
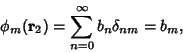 |
(13) |
so
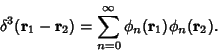 |
(14) |
By plugging in the differential operator, solving for the 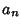 s, and substituting
into
s, and substituting
into 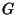 , the original nonhomogeneous equation then can be solved.
, the original nonhomogeneous equation then can be solved.
References
Arfken, G. ``Nonhomogeneous Equation--Green's Function,'' ``Green's Functions--One Dimension,'' and
``Green's Functions--Two and Three Dimensions.''
§8.7 and §16.5-16.6 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 480-491 and 897-924, 1985.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , then
, then
![]() in 3-D, the Green's function
in 3-D, the Green's function
![]() is defined by
analogy with the 1-D case by
is defined by
analogy with the 1-D case by