|
|
|

An Apodization Function, also called the Hann Function, frequently used to reduce Aliasing in
Fourier Transforms. The illustrations above show the Hanning function, its Instrument
Function, and a blowup of the Instrument Function sidelobes. The Hanning function is given by
| (1) |
| (2) |
![$\displaystyle \int_{-a}^a \left[{{\textstyle{1\over 2}}-{\textstyle{1\over 2}}\cos\left({\pi x\over a}\right)}\right]e^{-2\pi ikx}\,dx$](h_298.gif) |
|||
 |
|||
| (3) |
| (4) |
 |
|||
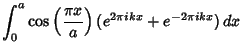 |
|||
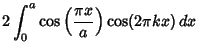 |
|||
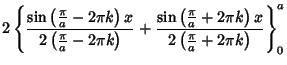 |
|||
![$\displaystyle a\left[{{\sin(\pi-2\pi ka)\over \pi-2\pi ka}+{\sin(\pi+2\pi ka)\over \pi+2\pi ka}}\right]$](h_307.gif) |
|||
![$\displaystyle {a\over\pi}\left[{{\sin(2\pi ka)\over 1-2ka}-{\sin(2\pi ka)\over 1+2ka}}\right]$](h_308.gif) |
|||
| (5) |
| (6) |
To find the extrema, define
![]() and rewrite (6) as
and rewrite (6) as
| (7) |
| (8) |
| (9) |
| (10) |
See also Apodization Function, Hamming Function
|
|
|
© 1996-9 Eric W. Weisstein