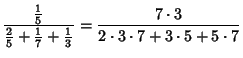An Apodization Function chosen to minimize the height of the highest sidelobe. The Hamming function is given
by
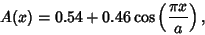 |
(1) |
Its Full Width at Half Maximum is 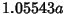 . The corresponding Instrument Function is
. The corresponding Instrument Function is
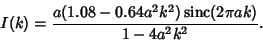 |
(2) |
This Apodization Function is close to the one produced by the requirement that the Apparatus Function goes
to 0 at 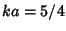 . From Apodization Function, a general symmetric apodization
function
. From Apodization Function, a general symmetric apodization
function 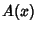 can be written as a
Fourier Series
can be written as a
Fourier Series
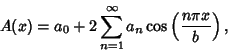 |
(3) |
where the Coefficients satisfy
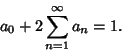 |
(4) |
The corresponding apparatus function is
![\begin{displaymath}
I(t)=2b\{a_0\mathop{\rm sinc}\nolimits (2\pi kb)+\sum_{n=1}^...
...s (2\pi kb+n\pi)+\mathop{\rm sinc}\nolimits (2\pi kb-n\pi)]\}.
\end{displaymath}](h_233.gif) |
(5) |
To obtain an Apodization Function with zero at  , use
, use
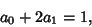 |
(6) |
so
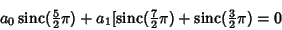 |
(7) |
 |
(8) |
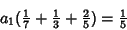 |
(9) |
The FWHM is 1.81522, the peak is 1.08, the peak Negative and Positive sidelobes (in units of the peak) are 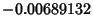 and 0.00734934, respectively.
and 0.00734934, respectively.
See also Apodization Function, Hanning Function, Instrument Function
References
Blackman, R. B. and Tukey, J. W. ``Particular Pairs of Windows.'' In
The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, pp. 98-99, 1959.
© 1996-9 Eric W. Weisstein
1999-05-25

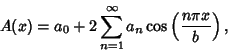
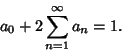
![\begin{displaymath}
I(t)=2b\{a_0\mathop{\rm sinc}\nolimits (2\pi kb)+\sum_{n=1}^...
...s (2\pi kb+n\pi)+\mathop{\rm sinc}\nolimits (2\pi kb-n\pi)]\}.
\end{displaymath}](h_233.gif)