A collection of equations satisfies the Hasse principle if, whenever one of the equations has solutions in 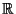 and
all the
and
all the 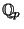 , then the equations have solutions in the
Rationals
, then the equations have solutions in the
Rationals 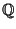 . Examples include the set of equations
. Examples include the set of equations
with 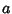 ,
, 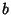 , and
, and 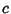 Integers, and the set of equations
Integers, and the set of equations
for 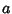 rational. The trivial solution
rational. The trivial solution 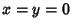 is usually not taken into account when deciding if a collection of
homogeneous equations satisfies the Hasse principle. The Hasse principle is sometimes called the
Local-Global Principle.
is usually not taken into account when deciding if a collection of
homogeneous equations satisfies the Hasse principle. The Hasse principle is sometimes called the
Local-Global Principle.
See also Local Field
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
all the
and
all the ![]() , then the equations have solutions in the
Rationals
, then the equations have solutions in the
Rationals ![]() . Examples include the set of equations
. Examples include the set of equations