In 2-D Polar Coordinates, attempt Separation of Variables by writing
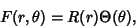 |
(1) |
then the Helmholtz Differential Equation becomes
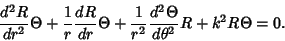 |
(2) |
Divide both sides by 
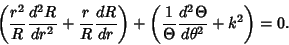 |
(3) |
The solution to the second part of (3) must be periodic, so the differential equation is
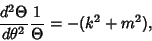 |
(4) |
which has solutions
Plug (4) back into (3)
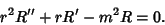 |
(6) |
This is an Euler Differential Equation with
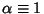 and
and
 . The roots are
. The roots are 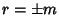 .
So for
.
So for 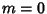 ,
, 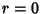 and the solution is
and the solution is
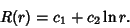 |
(7) |
But since 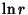 blows up at
blows up at 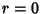 , the only possible physical solution is
, the only possible physical solution is 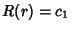 . When
. When 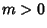 ,
, 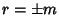 , so
, so
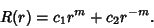 |
(8) |
But since 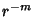 blows up at
blows up at 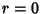 , the only possible physical solution is
, the only possible physical solution is
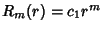 . The solution for
. The solution for 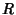 is
then
is
then
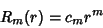 |
(9) |
for 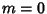 , 1, ...and the general solution is
, 1, ...and the general solution is
![\begin{displaymath}
F(r, \theta) = \sum_{m=0}^\infty [a_mr^m\sin (\sqrt{k^2+m^2}\,\theta)+b_mr^m\cos(\sqrt{k^2+m^2}\,\theta)].
\end{displaymath}](h_1103.gif) |
(10) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 502-504, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![\begin{displaymath}
F(r, \theta) = \sum_{m=0}^\infty [a_mr^m\sin (\sqrt{k^2+m^2}\,\theta)+b_mr^m\cos(\sqrt{k^2+m^2}\,\theta)].
\end{displaymath}](h_1103.gif)