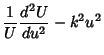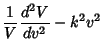In Parabolic Cylindrical Coordinates, the Scale Factors are
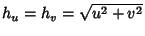 ,
,
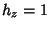 and the separation functions are
and the separation functions are
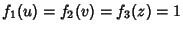 , giving Stäckel Determinant of
, giving Stäckel Determinant of 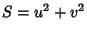 . The Helmholtz Differential Equation is
. The Helmholtz Differential Equation is
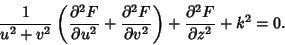 |
(1) |
Attempt Separation of Variables by writing
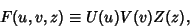 |
(2) |
then the Helmholtz Differential Equation becomes
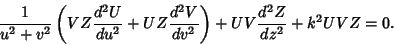 |
(3) |
Divide by  ,
,
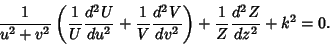 |
(4) |
Separating the  part,
part,
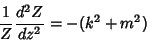 |
(5) |
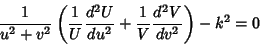 |
(6) |
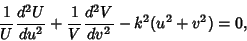 |
(7) |
so
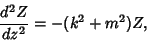 |
(8) |
which has solution
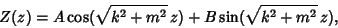 |
(9) |
and
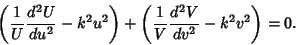 |
(10) |
This can be separated
so
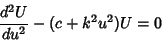 |
(13) |
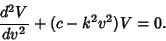 |
(14) |
These are the Weber Differential Equations, and the solutions are known as Parabolic Cylinder Functions.
See also Parabolic Cylinder Function, Parabolic Cylindrical Coordinates,
Weber Differential Equations
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 515 and 658, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
,
![]() and the separation functions are
and the separation functions are
![]() , giving Stäckel Determinant of
, giving Stäckel Determinant of ![]() . The Helmholtz Differential Equation is
. The Helmholtz Differential Equation is