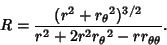 |
(1) |
Using
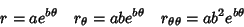 |
(2) |
gives
and
so
and the Tangent Vector is given by
The coordinates of the Evolute are therefore
So the Evolute is another logarithmic spiral with 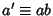 , as first shown by
Johann Bernoulli.
, as first shown by
Johann Bernoulli.  However, in some cases, the Evolute is identical to the original, as can be
demonstrated by making the substitution to the new variable
However, in some cases, the Evolute is identical to the original, as can be
demonstrated by making the substitution to the new variable
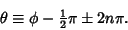 |
(9) |
Then the above equations become
which are equivalent to the form of the original equation if
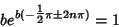 |
(12) |
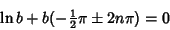 |
(13) |
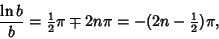 |
(14) |
where only solutions with the minus sign in 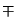 exist. Solving
gives the values summarized in the following table.
exist. Solving
gives the values summarized in the following table.
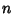 |
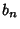 |
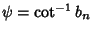 |
| 1 |
0.2744106319... |
 |
| 2 |
0.1642700512... |
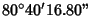 |
| 3 |
0.1218322508... |
 |
| 4 |
0.0984064967... |
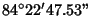 |
| 5 |
0.0832810611... |
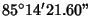 |
| 6 |
0.0725974881... |
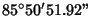 |
| 7 |
0.0645958183... |
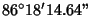 |
| 8 |
0.0583494073... |
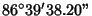 |
| 9 |
0.0533203211... |
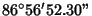 |
| 10 |
0.0491732529... |
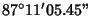 |
References
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press,
pp. 60-64, 1991.
© 1996-9 Eric W. Weisstein
1999-05-25
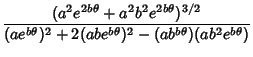
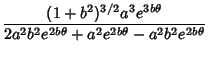
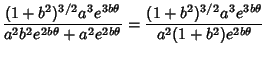
![$\displaystyle \left[\begin{array}{c}ae^{b\theta}\cos\theta\\ ae^{b\theta}\sin\theta\end{array}\right]$](l2_664.gif)
![$\displaystyle \left[\begin{array}{c}abe^{b\theta}\cos\theta-ae^{b\theta}\sin\theta\\
abe^{b\theta}\sin\theta+ae^{b\theta}\cos\theta\end{array}\right]\nonumber$](l2_666.gif)
![$\displaystyle ae^{b\theta}\left[\begin{array}{c}b\cos\theta-\sin\theta\\ b\sin\theta+\cos\theta\end{array}\right],$](l2_667.gif)
![$\displaystyle {{\bf r}'\over \vert{\bf r}'\vert} = {1\over ae^{b\theta} \sqrt{1...
...gin{array}{c}ae^{b\theta}\cos\theta\\ ae^{b\theta}\sin\theta\end{array}\right]$](l2_672.gif)
![$\displaystyle {1\over\sqrt{1+b^2}}\left[\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right].$](l2_673.gif)