|
|
|
An evolute is the locus of centers of curvature (the envelope) of a plane curve's normals. The original curve is then
said to be the Involute of its evolute. Given a plane curve represented parametrically by ![]() ,
the equation of the evolute is given by
,
the equation of the evolute is given by
| (1) | |||
| (2) |
| (3) |
| (4) |
| (5) | |||
| (6) |
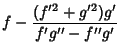 |
(7) | ||
 |
(8) |
The following table lists the evolutes of some common curves.
| Curve | Evolute |
| Astroid | Astroid 2 times as large |
| Cardioid | Cardioid 1/3 as large |
| Cayley's Sextic | Nephroid |
| Circle | point (0, 0) |
| Cycloid | equal Cycloid |
| Deltoid | Deltoid 3 times as large |
| Ellipse | Lamé Curve |
| Epicycloid | enlarged Epicycloid |
| Hypocycloid | similar Hypocycloid |
| Limaçon | Circle Catacaustic for a point source |
| Logarithmic Spiral | equal Logarithmic Spiral |
| Nephroid | Nephroid 1/2 as large |
| Parabola | Neile's Parabola |
| Tractrix | Catenary |
See also Involute, Osculating Circle
References
Cayley, A. ``On Evolutes of Parallel Curves.'' Quart. J. Pure Appl. Math. 11, 183-199, 1871.
Dixon, R. ``String Drawings.'' Ch. 2 in Mathographics. New York: Dover, pp. 75-78, 1991.
Gray, A. ``Evolutes.'' §5.1 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 76-80, 1993.
Jeffrey, H. M. ``On the Evolutes of Cubic Curves.'' Quart. J. Pure Appl. Math. 11, 78-81 and 145-155, 1871.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 40 and 202, 1972.
Lee, X. ``Evolute.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Evolute_dir/evolute.html.
Lockwood, E. H. ``Evolutes and Involutes.'' Ch. 21 in A Book of Curves. Cambridge, England: Cambridge
University Press, pp. 166-171, 1967.
Yates, R. C. ``Evolutes.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 86-92, 1952.
|
|
|
© 1996-9 Eric W. Weisstein