|
|
|

The Circle which shares the same Tangent as a curve at a given point. The Radius of Curvature of
the osculating circle is
| (1) |
 |
(2) | ||
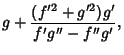 |
(3) |
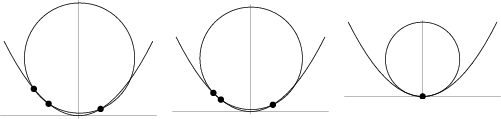
In addition, let
![]() denote the Circle passing through three points on a curve
denote the Circle passing through three points on a curve ![]() with
with
![]() . Then the osculating circle
. Then the osculating circle ![]() is given by
is given by
| (4) |
See also Curvature, Evolute, Radius of Curvature, Tangent
References
Gardner, M. ``The Game of Life, Parts I-III.'' Chs. 20-22 in Wheels, Life, and other Mathematical Amusements.
New York: W. H. Freeman, pp. 221, 237, and 243, 1983.
Gray, A. ``Osculating Circles to Plane Curves.'' §5.6 in
Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 90-95, 1993.