|
|
|
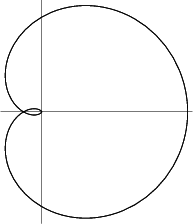
A plane curve discovered by Maclaurin but first studied in detail by Cayley. ![]() The name Cayley's sextic is due
to R. C. Archibald, who attempted to classify curves in a paper published in Strasbourg in 1900 (MacTutor Archive).
Cayley's sextic is given in Polar Coordinates by
The name Cayley's sextic is due
to R. C. Archibald, who attempted to classify curves in a paper published in Strasbourg in 1900 (MacTutor Archive).
Cayley's sextic is given in Polar Coordinates by
| (1) |
| (2) |
| (3) |
| (4) | |||
| (5) |

The Arc Length, Curvature, and Tangential Angle are
| (6) | |||
| (7) | |||
| (8) |
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 178 and 180, 1972.
MacTutor History of Mathematics Archive. ``Cayley's Sextic.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cayleys.html.