|
|
|

The cycloid is the locus of a point on the rim of a Circle of Radius ![]() rolling along a straight
Line. It was studied and named by Galileo
rolling along a straight
Line. It was studied and named by Galileo ![]() in 1599. Galileo attempted to find the Area by
weighing pieces of metal cut into the shape of the cycloid. Torricelli,
in 1599. Galileo attempted to find the Area by
weighing pieces of metal cut into the shape of the cycloid. Torricelli, ![]() Fermat,
Fermat, ![]() and
Descartes
and
Descartes ![]() all found the Area. The cycloid was also studied by Roberval in 1634, Wren in 1658,
Huygens
all found the Area. The cycloid was also studied by Roberval in 1634, Wren in 1658,
Huygens ![]() in 1673, and Johann Bernoulli
in 1673, and Johann Bernoulli ![]() in 1696. Roberval and Wren found the
Arc Length (MacTutor Archive). Gear teeth were also made out of cycloids, as first proposed by Desargues in the
1630s (Cundy and Rollett 1989).
in 1696. Roberval and Wren found the
Arc Length (MacTutor Archive). Gear teeth were also made out of cycloids, as first proposed by Desargues in the
1630s (Cundy and Rollett 1989).
In 1696, Johann Bernoulli ![]() challenged other mathematicians to find the curve which solves the
Brachistochrone Problem, knowing the solution to be a cycloid. Leibniz,
challenged other mathematicians to find the curve which solves the
Brachistochrone Problem, knowing the solution to be a cycloid. Leibniz, ![]() Newton,
Newton, ![]() Jakob Bernoulli
Jakob Bernoulli ![]() and L'Hospital
and L'Hospital ![]() all solved Bernoulli's challenge.
The cycloid also solves the Tautochrone Problem. Because of the frequency with which it provoked quarrels among
mathematicians in the 17th century, the cycloid became known as the ``Helen of Geometers'' (Boyer 1968, p. 389).
all solved Bernoulli's challenge.
The cycloid also solves the Tautochrone Problem. Because of the frequency with which it provoked quarrels among
mathematicians in the 17th century, the cycloid became known as the ``Helen of Geometers'' (Boyer 1968, p. 389).
The cycloid is the Catacaustic of a Circle for a Radiant Point on the circumference, as shown by Jakob and Johann Bernoulli in 1692. The Caustic of the cycloid when the rays are parallel to the y-Axis is a cycloid with twice as many arches. The Radial Curve of a Cycloid is a Circle. The Evolute and Involute of a cycloid are identical cycloids.
If the cycloid has a Cusp at the Origin, its equation in Cartesian Coordinates is
| (1) |
| (2) | |||
| (3) |
| (4) |
| (5) | |||
| (6) |
The Derivatives of the parametric representation (2) and
(3) are
| (7) | |||
| (8) |
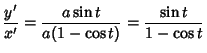 |
|||
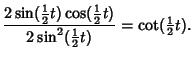 |
(9) |
| (10) | |||
| (11) |
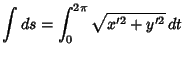 |
|||
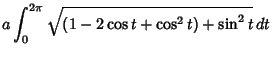 |
|||
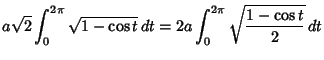 |
|||
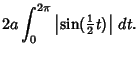 |
(12) |
![$\displaystyle 4a\int_0^\pi \sin u\, du= 4a[-\cos u]^{\pi}_0$](c4_858.gif) |
|||
| (13) |

The Arc Length, Curvature, and Tangential Angle are
| (14) | |||
| (15) | |||
| (16) |
The Area under a single cycle is
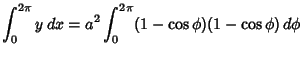 |
|||
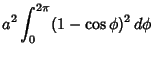 |
|||
 |
|||
![$\displaystyle a^2\int_0^{2\pi} \{1-2\cos\phi+{\textstyle{1\over 2}}[1+\cos(2\phi)]\}\,d\phi$](c4_868.gif) |
|||
![$\displaystyle a^2\int_0^{2\pi} [{\textstyle{3\over 2}} -2\cos \phi +{\textstyle{1\over 2}}\cos (2\phi)]\,d\phi$](c4_869.gif) |
|||
| (17) |
The Normal is
| (18) |
See also Curtate Cycloid, Cyclide, Cycloid Evolute, Cycloid Involute, Epicycloid, Hypocycloid, Prolate Cycloid, Trochoid
References
Bogomolny, A. ``Cycloids.''
http://www.cut-the-knot.com/pythagoras/cycloids.html.
Boyer, C. B. A History of Mathematics. New York: Wiley, 1968.
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., 1989.
Gray, A. ``Cycloids.'' §3.1 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 37-39, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 192 and 197, 1972.
Lee, X. ``Cycloid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Cycloid_dir/cycloid.html.
Lockwood, E. H. ``The Cycloid.'' Ch. 9 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 80-89, 1967.
MacTutor History of Mathematics Archive. ``Cycloid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cycloid.html.
Muterspaugh, J.; Driver, T.; and Dick, J. E. ``The Cycloid and Tautochronism.''
http://php.indiana.edu/~jedick/project/intro.html.
Pappas, T. ``The Cycloid--The Helen of Geometry.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra,
pp. 6-8, 1989.
Wagon, S. ``Rolling Circles.'' Ch. 2 in Mathematica in Action. New York: W. H. Freeman, pp. 39-66, 1991.
Yates, R. C. ``Cycloid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 65-70, 1952.
|
|
|
© 1996-9 Eric W. Weisstein