|
|
|
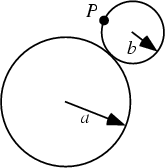
The path traced out by a point ![]() on the Edge of a Circle of Radius
on the Edge of a Circle of Radius ![]() rolling on the
outside of a Circle of Radius
rolling on the
outside of a Circle of Radius ![]() .
.
It is given by the equations
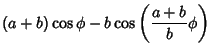 |
(1) | ||
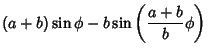 |
(2) |
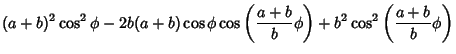 |
(3) | ||
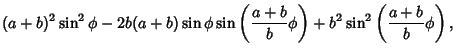 |
(4) |
|
|
|
|
|
(5) |
| (6) |
| (7) |
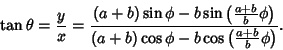 |
(8) |
To get ![]() Cusps in the epicycloid,
Cusps in the epicycloid, ![]() , because then
, because then ![]() rotations of
rotations of ![]() bring the point on
the edge back to its starting position.
bring the point on
the edge back to its starting position.
![$\displaystyle a^2\left[{\left({1+{1\over n}}\right)^2+\left({1\over n}\right)^2-2\left({1\over n}\right)\left({1+{1\over n}}\right)\cos (n\phi )}\right]$](e_1485.gif) |
|||
![$\displaystyle a^2\left[{1+{2\over n}+{1\over n^2}+{1\over n^2}-\left({2\over n}\right)\left({n+1\over n}\right)\cos (n\phi )}\right]$](e_1486.gif) |
|||
![$\displaystyle a^2\left[{{n^2+2n+2\over n^2}-{2(n+1)\over n^2}\cos (n\phi )}\right]$](e_1487.gif) |
|||
![$\displaystyle {a^2\over n^2}\left[{(n^2+2n+2)-2(n+1)\cos (n\phi)}\right],$](e_1488.gif) |
(9) |
![$\displaystyle {a\left({n+1\over n}\right)\sin\phi-{a\over n}\sin[(n+1)\phi]\over a\left({n+1\over n}\right)\cos\phi-{a\over n}\cos[(n+1)\phi]}$](e_1489.gif) |
|||
![$\displaystyle {(n+1)\sin\phi-\sin[(n+1)\phi]\over(n+1)\cos\phi-\cos[(n+1)\phi]}.$](e_1490.gif) |
(10) |
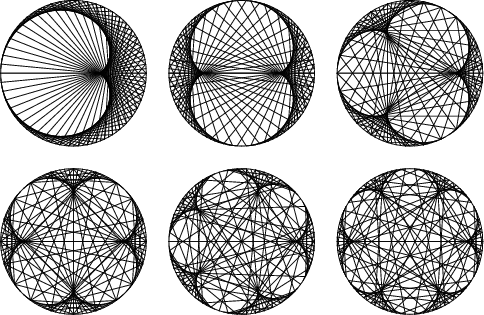
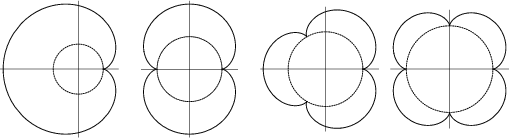
![]() -epicycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end
by a series of steps while at the same time offsetting the other end by steps
-epicycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end
by a series of steps while at the same time offsetting the other end by steps ![]() times as large. After traveling around
the Circle once, an
times as large. After traveling around
the Circle once, an ![]() -cusped epicycloid is produced, as illustrated above (Madachy 1979).
-cusped epicycloid is produced, as illustrated above (Madachy 1979).
Epicycloids have Torsion
| (11) |
| (12) |
See also Cardioid, Cyclide, Cycloid, Epicycloid--1-Cusped, Hypocycloid, Nephroid, Ranunculoid
References
Bogomolny, A. ``Cycloids.''
http://www.cut-the-knot.com/pythagoras/cycloids.html.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 160-164 and 169, 1972.
Lee, X. ``Epicycloid and Hypocycloid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypocycloid_dir/epiHypocycloid.html.
MacTutor History of Mathematics Archive. ``Epicycloid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Epicycloid.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 219-225, 1979.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991.
Yates, R. C. ``Epi- and Hypo-Cycloids.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 81-85, 1952.
|
|
|
© 1996-9 Eric W. Weisstein