|
|
|
The curve produced by a small Circle of Radius ![]() rolling around the inside of a large Circle of
Radius
rolling around the inside of a large Circle of
Radius ![]() . A hypocycloid is a Hypotrochoid with
. A hypocycloid is a Hypotrochoid with ![]() . To derive the equations of the hypocycloid, call the
Angle by which a point on the small Circle rotates about its center
. To derive the equations of the hypocycloid, call the
Angle by which a point on the small Circle rotates about its center ![]() , and the Angle from the
center of the large Circle to that of the small Circle
, and the Angle from the
center of the large Circle to that of the small Circle ![]() . Then
. Then
| (1) |
| (2) |
 |
(3) | ||
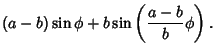 |
(4) |
If ![]() instead so the first point is at maximum radius (on the Circle), then the equations of the
hypocycloid are
instead so the first point is at maximum radius (on the Circle), then the equations of the
hypocycloid are
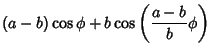 |
(5) | ||
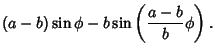 |
(6) |
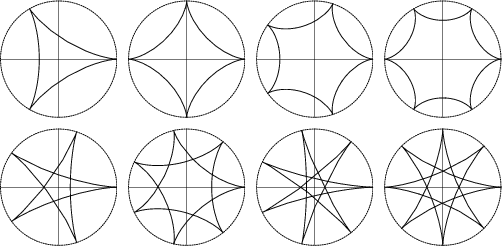
An ![]() -cusped non-self-intersecting hypocycloid has
-cusped non-self-intersecting hypocycloid has ![]() . A 2-cusped hypocycloid is a Line Segment, as can be seen
by setting
. A 2-cusped hypocycloid is a Line Segment, as can be seen
by setting ![]() in equations (3) and (4) and noting that the equations simplify to
in equations (3) and (4) and noting that the equations simplify to
| (7) | |||
| (8) |
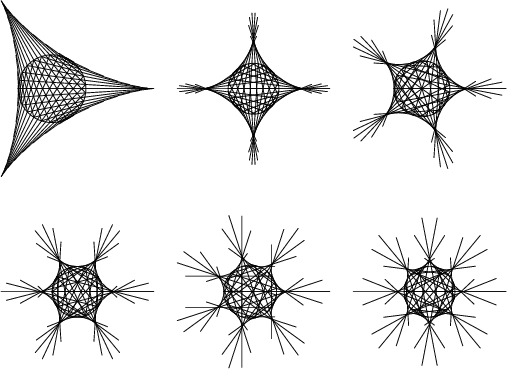
![]() -hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by a
series of steps while at the same time offsetting the other end by steps
-hypocycloids can also be constructed by beginning with the Diameter of a Circle, offsetting one end by a
series of steps while at the same time offsetting the other end by steps ![]() times as large in the opposite direction and
extending beyond the edge of the Circle. After traveling around the Circle once, an
times as large in the opposite direction and
extending beyond the edge of the Circle. After traveling around the Circle once, an ![]() -cusped hypocycloid is
produced, as illustrated above (Madachy 1979).
-cusped hypocycloid is
produced, as illustrated above (Madachy 1979).
Let ![]() be the radial distance from a fixed point. For Radius of Torsion
be the radial distance from a fixed point. For Radius of Torsion ![]() and Arc Length
and Arc Length ![]() , a hypocycloid
can given by the equation
, a hypocycloid
can given by the equation
| (9) |
| (10) |
| (11) |
The Arc Length of the hypocycloid can be computed as follows
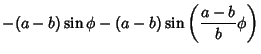 |
|||
![$\displaystyle (a-b)\left[{\sin\phi+\sin\left({{a-b\over b}\phi}\right)}\right]$](h_2478.gif) |
(12) | ||
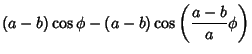 |
|||
![$\displaystyle (a-b)\left[{\cos\phi-\cos\left({{a-b\over b}\phi}\right)}\right]$](h_2480.gif) |
(13) |
|
|
|
|
|
|
|
|
|
|
|
(14) |
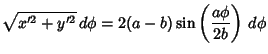 |
(15) |
![$\displaystyle \int_0^\phi ds=2(a-b)\left[{-{2b\over a}\cos\left({a\phi\over 2b}\right)}\right]_0^\phi$](h_2489.gif) |
|||
![$\displaystyle {4b(a-b)\over a}\left[{-\cos\left({{a\over 2b}\phi}\right)+1}\right]$](h_2490.gif) |
|||
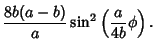 |
(16) |
| (17) |
| (18) | |||
| (19) |
| (20) |
Compute
\left[{\sin \phi+\sin\left({{a-b\over b} \phi}\right)}\right]$](h_2498.gif) |
|||
\left[{\cos \phi-\cos\left({{a-b\over b} \phi}\right)}\right]$](h_2499.gif) |
|||
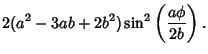 |
(21) |
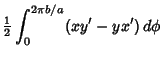 |
|||
![$\displaystyle (a^2-3ab+2b^2)\left[{at-b\sin\left({at\over b}\right)\over 2a}\right]^{2\pi b/a}_a$](h_2502.gif) |
|||
![$\displaystyle (a^2-3ab+2b^2)\left[{a\left({2\pi{b\over a}}\right)\over 2a}\right]$](h_2503.gif) |
|||
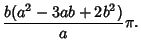 |
(22) |
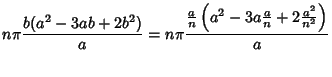 |
|||
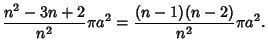 |
(23) |
The equation of the hypocycloid can be put in a form which is useful in the solution of Calculus of
Variations problems with radial symmetry. Consider the case ![]() , then
, then
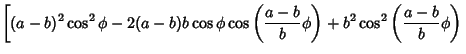 |
|||
![$\displaystyle \mathop{+} \left.{(a-b)^2\sin^2\phi+2(a-b)b\sin\phi\sin\left({{a-b\over b}\phi}\right)+b^2\sin^2\left({{a-b\over b}\phi}\right)}\right]$](h_2512.gif) |
|||
![$\displaystyle \left\{{(a-b)^2+b^2-2(a-b)b}\left[{\cos\phi\cos\left({{a-b\over b}\phi}\right)-\sin\phi\sin\left({{a-b\over b}\phi}\right)}\right]\right\}$](h_2513.gif) |
|||
| (24) |
| (25) | |||
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
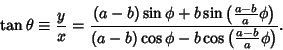 |
(31) |
| (32) | |||
| (33) | |||
| (34) |
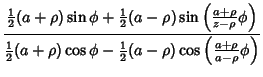 |
|||
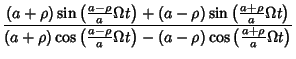 |
|||
![$\displaystyle {a\left[{\sin\left({{a-\rho\over a}\Omega t}\right)+\sin\left({{a...
...ho\over a} \Omega t}\right)+\cos\left({{a+\rho\over a}\Omega t}\right)}\right]}$](h_2539.gif) |
|||
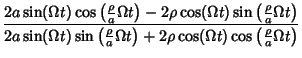 |
|||
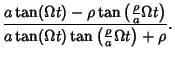 |
(35) |
Computing
![$\displaystyle {\left[{a\tan(\Omega t)-\rho\tan\left({{\rho\over a}\Omega t}\rig...
...{{\rho\over a}\Omega t}\right)}\right]\tan\left({{\rho\over a}\Omega t}\right)}$](h_2543.gif) |
|||
![$\displaystyle {a\tan(\Omega t)\left[{1+\tan^2\left({{\rho\over a}\Omega t}\right)}\right]\over\rho\left[{1+\tan^2\left({{\rho\over a}\Omega t}\right)}\right]}$](h_2544.gif) |
|||
| (36) |
then gives
| (37) |
![$\displaystyle \tan^{-1}\left[{{a\over\rho}\tan\left({{a\over a-\rho}\phi}\right)}\right]-{\rho\over a}{a\over a-\rho} \phi$](h_2548.gif) |
|||
![$\displaystyle \tan^{-1}\left[{{a\over\rho}\tan\left({{a\over a-\rho}\phi}\right)}\right]-{\rho\over a-\rho}\phi.$](h_2549.gif) |
(38) |
See also Cycloid, Epicycloid
References
Bogomolny, A. ``Cycloids.''
http://www.cut-the-knot.com/pythagoras/cycloids.html.
Kreyszig, E. Differential Geometry. New York: Dover, 1991.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 171-173, 1972.
Lee, X. ``Epicycloid and Hypocycloid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypocycloid_dir/epiHypocycloid.html.
MacTutor History of Mathematics Archive. ``Hypocycloid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hypocycloid.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 225-231, 1979.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991.
Yates, R. C. ``Epi- and Hypo-Cycloids.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 81-85, 1952.
|
|
|
© 1996-9 Eric W. Weisstein