|
|
|
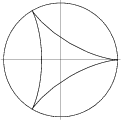
|
A 3-cusped Hypocycloid, also called a Tricuspoid, which has ![]() or
or ![]() , where
, where ![]() is the
Radius of the large fixed Circle and
is the
Radius of the large fixed Circle and ![]() is the Radius of the small rolling Circle. The deltoid
was first considered by Euler
is the Radius of the small rolling Circle. The deltoid
was first considered by Euler ![]() in 1745 in connection with an optical problem. It was also investigated by Steiner
in 1856 and is sometimes called Steiner's Hypocycloid (MacTutor Archive). The equation of the deltoid is obtained by
setting
in 1745 in connection with an optical problem. It was also investigated by Steiner
in 1856 and is sometimes called Steiner's Hypocycloid (MacTutor Archive). The equation of the deltoid is obtained by
setting ![]() in the equation of the Hypocycloid, yielding the parametric equations
in the equation of the Hypocycloid, yielding the parametric equations
| (1) | |||
| (2) |

The Arc Length, Curvature, and Tangential Angle are
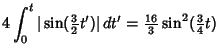 |
(3) | ||
| (4) | |||
| (5) |
| (6) |
| (7) |
The total Arc Length is computed from the general Hypocycloid equation
| (8) |
| (9) |
| (10) |
| (11) |
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, p. 53, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 131-135, 1972.
Lee, X. ``Deltoid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Deltoid_dir/deltoid.html.
Lockwood, E. H. ``The Deltoid.'' Ch. 8 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 72-79, 1967.
Macbeth, A. M. ``The Deltoid, I.'' Eureka 10, 20-23, 1948.
Macbeth, A. M. ``The Deltoid, II.'' Eureka 11, 26-29, 1949.
Macbeth, A. M. ``The Deltoid, III.'' Eureka 12, 5-6, 1950.
MacTutor History of Mathematics Archive. ``Tricuspoid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Tricuspoid.html.
Yates, R. C. ``Deltoid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 71-74, 1952.
|
|
|
© 1996-9 Eric W. Weisstein