|
|
|
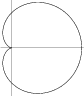
|
The curve given by the Polar equation
| (1) |
| (2) |
| (3) |
| (4) | |||
| (5) |
The name cardioid was first used by de Castillon in Philosophical Transactions of the Royal Society in 1741. Its
Arc Length was found by La Hire in 1708. There are exactly three Parallel Tangents to
the cardioid with any given gradient. Also, the Tangents at the ends of any Chord through the
Cusp point are at Right Angles. The length of any Chord through the Cusp point
is ![]() .
.
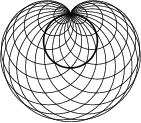
|
The cardioid may also be generated as follows. Draw a Circle ![]() and fix a point
and fix a point ![]() on it. Now draw a set of
Circles centered on the Circumference of
on it. Now draw a set of
Circles centered on the Circumference of ![]() and passing through
and passing through ![]() . The Envelope of
these Circles is then a cardioid (Pedoe 1995). Let the Circle
. The Envelope of
these Circles is then a cardioid (Pedoe 1995). Let the Circle ![]() be centered at the origin and
have Radius 1, and let the fixed point be
be centered at the origin and
have Radius 1, and let the fixed point be ![]() . Then the Radius of a Circle centered at an
Angle
. Then the Radius of a Circle centered at an
Angle ![]() from (1, 0) is
from (1, 0) is
| (6) |

The Arc Length, Curvature, and Tangential Angle are
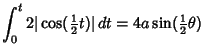 |
(7) | ||
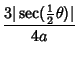 |
(8) | ||
| (9) |
| (10) |
| (11) |
The Perimeter of the curve is
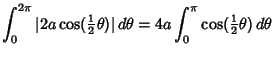 |
|||
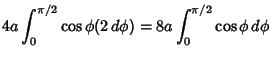 |
|||
| (12) |
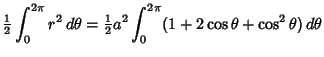 |
|||
![$\displaystyle {\textstyle{1\over 2}}a^2 \int_0^{2\pi} \{1+2\cos \theta +{\textstyle{1\over 2}}[1+\cos (2\theta)]\}\,d\theta$](c1_161.gif) |
|||
![$\displaystyle {\textstyle{1\over 2}}a^2 \int_0^{2\pi} [{\textstyle{3\over 2}}+2\cos\theta +{\textstyle{1\over 2}}\cos(2\theta)]\,d\theta$](c1_162.gif) |
|||
| (13) |
See also Circle, Cissoid, Conchoid, Equiangular Spiral, Lemniscate, Limaçon, Mandelbrot Set
References
Gray, A. ``Cardioids.'' §3.3 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 41-42, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 118-121, 1972.
Lee, X. ``Cardioid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Cardioid_dir/cardioid.html.
Lee, X. ``Cardioid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Cardioid_dir/cardioidGG.html.
Lockwood, E. H. ``The Cardioid.'' Ch. 4 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 34-43, 1967.
MacTutor History of Mathematics Archive. ``Cardioid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cardioid.html.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., pp. xxvi-xxvii, 1995.
Yates, R. C. ``The Cardioid.'' Math. Teacher 52, 10-14, 1959.
Yates, R. C. ``Cardioid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 4-7, 1952.
|
|
|
© 1996-9 Eric W. Weisstein