|
|
|

The set obtained by the Quadratic Recurrence
| (1) |
J. Hubbard and A. Douady proved that the Mandelbrot set is Connected. Shishikura (1994) proved that the boundary of the Mandelbrot set is a Fractal with Hausdorff Dimension 2. However, it is not yet known if the Mandelbrot set is pathwise-connected. If it is pathwise-connected, then Hubbard and Douady's proof implies that the Mandelbrot set is the image of a Circle and can be constructed from a Disk by collapsing certain arcs in the interior (Douady 1986).
The Area of the set is known to lie between 1.5031 and 1.5702; it is estimated as 1.50659....
Decomposing the Complex coordinate ![]() and
and ![]() gives
gives
| (2) | |||
| (3) |
| (4) |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) |
| (9) | |||
| (10) | |||
| (11) |
| (12) |
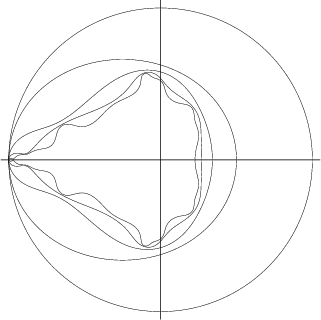
The kidney bean-shaped portion of the Mandelbrot set is bordered by a Cardioid with equations
| (13) |
| (14) |
Generalizations of the Mandelbrot set can be constructed by replacing ![]() with
with ![]() or
or ![]() , where
, where
![]() is a Positive Integer and
is a Positive Integer and ![]() denotes the Complex Conjugate of
denotes the Complex Conjugate of ![]() . The following figures show the
Fractals obtained for
. The following figures show the
Fractals obtained for ![]() , 3, and 4 (Dickau). The plots on the right have
, 3, and 4 (Dickau). The plots on the right have ![]() replaced with
replaced with ![]() and are sometimes called ``Mandelbar Sets.''
and are sometimes called ``Mandelbar Sets.''
 |
 |
 |
 |
 |
 |
See also Cactus Fractal, Fractal, Julia Set, Lemniscate (Mandelbrot Set), Mandelbar Set, Quadratic Map, Randelbrot Set, Sea Horse Valley
References
Alfeld, P. ``The Mandelbrot Set.''
http://www.math.utah.edu/~alfeld/math/mandelbrot/mandelbrot1.html.
Branner, B. ``The Mandelbrot Set.'' In Chaos and Fractals: The Mathematics Behind the Computer Graphics,
Proc. Sympos. Appl. Math., Vol. 39 (Ed. R. L. Devaney and L. Keen). Providence, RI: Amer. Math. Soc., 75-105, 1989.
Dickau, R. M. ``Mandelbrot (and Similar) Sets.''
http://forum.swarthmore.edu/advanced/robertd/mandelbrot.html.
Douady, A. ``Julia Sets and the Mandelbrot Set.'' In The Beauty of Fractals: Images of Complex Dynamical Systems
(Ed. H.-O. Peitgen and D. H. Richter). Berlin: Springer-Verlag, p. 161, 1986.
Eppstein, D. ``Area of the Mandelbrot Set.''
http://www.ics.uci.edu/~eppstein/junkyard/mand-area.html.
Fisher, Y. and Hill, J. ``Bounding the Area of the Mandelbrot Set.'' Submitted.
Hill, J. R. ``Fractals and the Grand Internet Parallel Processing Project.'' Ch. 15 in Fractal Horizons:
The Future Use of Fractals. New York: St. Martin's Press, pp. 299-323, 1996.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press,
pp. 148-151 and 179-180, 1991.
Munafo, R. ``Mu-Ency--The Encyclopedia of the Mandelbrot Set.''
http://home.earthlink.net/~mrob/muency.html.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, pp. 178-179, 1988.
Shishikura, M. ``The Boundary of the Mandelbrot Set has Hausdorff Dimension Two.'' Astérisque, No. 222, 7, 389-405, 1994.
|
|
|
© 1996-9 Eric W. Weisstein